Alain Bouquet - Gravitation quantique

⬄ la gravité n’est pas une force mais une accélération comme les forces centrifuges, la force de Coriolis, ou celle qui vous envoie dans le pare-brise lors d’un coup de frein

⬄ elle n’existe pas dans le « bon » référentiel…

⬄ la gravité n’est pas une propriété de l’objet mais une propriété du lieu

⬄ elle peut entièrement s’interpréter comme une courbure de l’espace-temps

⬄ dans lequel un objet suit la trajectoire la plus droite possible (géodésique)

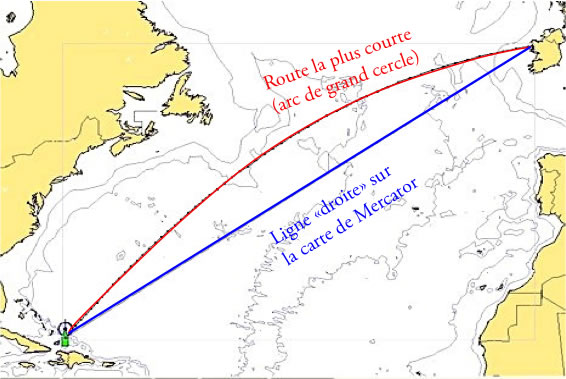
Analogie terrestre: la ligne la plus droite sur Terre est un arc de grand cercle, et non la ligne droite sur une carte de Mercator

Géodésique terrestre: l'arc de grand cercle

La Relativité Générale: une hydre à deux têtes

La Relativité Générale d'Einstein comporte deux volets indépendants Hydre à deux têtes

un aspect géométrique
un aspect dynamique

Géométrie ⇔ métrique g_μν

La métrique n'est qu'une généralisation du théorème de Pythagore !

∂s2 = Σ g_μν ∂x^μ ∂x^ν

g_μν ➟ R_μνρσ (tenseur de Riemann) ➟ R_μν (tenseur de Ricci) ➟ R (scalaire de Ricci)

➟ G_μν (tenseur d’Einstein)

Dynamique ⇔ matière T_μν

Matière ordinaire (étoiles, tables…)
Matière extraordinaire (noire…)
Rayonnements en tous genres
Énergie noire

➟ T_μν (tenseur énergie-impulsion)

Équation d'Einstein : G_μν = T_μν

Lagrangien de la relativité générale

L = ∫d4x R(gμν)

Modifier la relativité générale

changer la partie « géométrie »
- ➛ constante cosmologique Λ
- ➛ tenseur plus complexe que G
- ➛ termes en R2…
- ➛ dimensions supplémentaires
changer la partie matière
- ➛ nouveaux champs de matière
- ➛ énergie du vide (énergie noire)

Aucune indication expérimentale allant au-delà de la relativité générale la plus simple (sauf pour Λ ⬄ énergie noire)

Les unités de Planck (1899)

À partir des trois constantes fondamentales de la physique

la vitesse « de la lumière » c dimension LT^–1 (longueur/temps)
la constante de Planck ħ dimension ML²T^–1 (énergie•temps)
la constante de Newton G dimension M^–1L³T^–2 (accélération•longueur²/masse)

il est possible de construire un système « fondamental » d’unités

L_Planck = [ħ G/c³] ^½ = 1.616x10^–35 m
M_Planck = [ħ c/G] ^½ = 2.177x10^–8 kg
T_Planck = [ħ G/c⁵] ^½ = 5.391x10^–44 s

➡ unités dérivées comme l'énergie de Planck E_Planck = [ħ c⁵/G] ^½ = 10¹⁹ GeV = 1.956x10⁹ J

➡ idée : les effets quantiques de la gravitation sont importants quand on approche de l’échelle de Planck (énergies > 10¹⁹ GeV, distances < 10^–35 m, durées < 10^–44 s)

Quantifier la gravitation?

Pourquoi vouloir quantifier la gravitation (et en particulier la relativité générale) alors qu'aucun indice expérimental ne le justifie?

La matière et le rayonnement sont quantifiés dans le cadre unificateur de la théorie quantique des champs, tandis que la relativité générale est une théorie non-quantique.
C'est une différence irréductible avec les 3 autres interactions (électromagnétique, nucléaire forte et nucléaire faible)
À l'échelle de Planck, il est plausible que la gravitation elle-même doive être décrite de manière quantique

On peut imaginer une théorie classique de l’espace-temps avec des champs de matière quantiques, autrement dit une théorie quantique de la matière (et du rayonnement) en espace-temps courbe

➛ entropie des trous noirs
➛ rayonnement Hawking
➛ rayonnement Unruh
➛ théorie du big bang chaud

L = ∫d⁴x {∂_μφ ∂^μφ +…} ➛ L = ∫d⁴x {g_μν ∂^μφ ∂^νφ +…}

l’espace-temps est fixé a priori via g_μν
les solutions obtenues pour les champs de matière (φ, A_μ…) diffèrent selon que l’espace est plat (Minkowski), en expansion (Robertson-Walker), au voisinage d’une masse (Schwarzschild)

Cela revient à modifier l'équation d'Einstein G_μν = T_μν en G_μν = <T_μν> en faisant apparaître la valeur moyenne dans le vide (v.e.v.) du tenseur énergie-impusion

Inconvénients:

seules les v.e.v. des champs de matière sont déterminés
<T_μν> dépend non-linéairement de la matière

Une idée récurrente est qu'une éventuelle diiscrétisation de l’espace-temps entraînerait une coupure (cut-off) naturelle des divergences ultraviolette de la théorie quantique (énergie-impulsion tendant vers l'infini correspondant aux distances tendant vers zéro). Deux approches intègrent une telle discrétisation:

la théorie des cordes
la théorie des boucles

Ces deux approches sont orthogonales

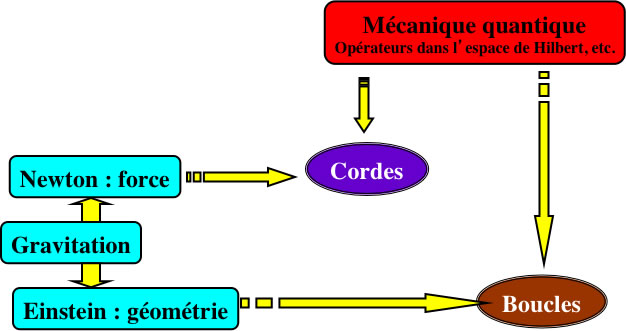
Deux voies vers la gravitation quantique

La gravitation comme théorie des champs banale?

Le point de départ est une linéarisation (indispensable)

g_μν = η_μν + h_μν

où η_μν est une métrique fixée a priori, dite d’arrière-plan (background metric) qui peut être celle de Minkowski, de Schwarzschild, de Robertson-Walker, etc.

et h_μν est un champ décrivant des fluctuations, en principe petites, autour de la métrique d'arrière plan. C'est ce champ qui est quantifié

quanta de spin 2 et masse nulle
auto-interactif avec un couplage √G_Newton

La construction de cette théorie fut longue et difficile

Rosenfeld (1930), Pauli & Fierz (1939), Gupta (1952)
Feynman (1963) : théorie à l’ordre zéro = RG linéarisée, mais unitarité violée à une boucle
DeWitt (1964-1967) : unitarité à une boucle [avec « fantômes » de Fadeev-Popov]
t’Hooft [1973] : divergence à une boucle et non-renormalisabilité
Stelle (1977) : renormalisabilité à une boucle mais au prix de l’unitarité
Compensation fermion-boson des divergences par supersymétrie (1976)
Plusieurs supersymétries : supergravité N=8 (Cremmer-Julia-Scherk 1978) équivalente à N=1 en 11 dimensions

Cette dernière théorie parut alors si élégante que Hawking déclara en 1980 la physique achevée. En 1984, tout ceci fut (provisoirement) oublié au profit d'une théorie toute différente, la théorie des cordes.

Cordes et branes

Les divergences empoisonnant la théorie quantique des champs venant du caractère ponctuel des particules, l'idée est remplacer celles-ci par des objets étendus. La théorie des cordes postule que l'objet fondamental n'est pas ponctuel (particule) mais étendu, à une dimension (corde) ou plusieurs (brane).

Cordes

L'action d'une particule libre est proportionnelle à la longueur de la ligne d'univers qu'elle parcourt dans son mouvement. Il est donc naturel de supposer que l'action d'une corde libre ouverte soit proportionnelle à la surface d'univers qu'elle balaie dans son mouvement (action de Polyakov).

Un point de la surface d'univers (bi-dimensionnelle) est déterminé par deux coordonnées s = {s₁,s₂} et la géométrie de cette surface par un tenseur 2x2 hab. La position de la corde dans l'espace-temps est donnée par les coordonnées X_m, et la géométrie de cet espace-temps par un tenseur métrique g_mn. Aucune hypothèse n'est faite à priori sur le nombre D de dimensions de l'espace-temps, ni sur sa géométrie.

Cette action est identique à celle qu'on aurait éécrite pour un modèle de théorie quantique des champs (modèle sigma en 2 dimensions d'espace-temps) décrivant D champs scalaires X_m)

On peut donc utiliser tout l’arsenal des théories conformes et des modèles sigma non-linéaires.

Avantage : le spectre d'excitations le long d ’une corde fermée contient un état de spin 2 et de masse nulle (description possible d’un graviton ? )

Inconvénients: les états quantique n'ont une norme positive que si D=26 dimensions. Le premier état quantique est par ailleurs un tachyon (particule de masse carrée négative).

Une interaction de cordes est une scission ou une fusion de cordes.

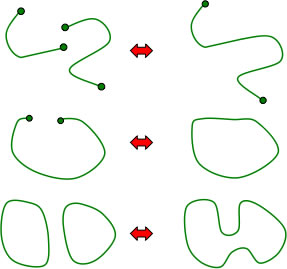
Interaction de cordes

Cette scission ou fusion n'est pas localisée dans l'espace-temps.

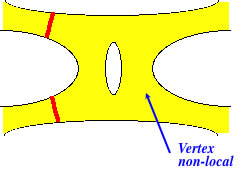
Vertex d'interaction de cordes

Intérêt

Particules ponctuelles ⬄distances ➛ 0

⬄ énergies ➛ ∞ ⬄ divergences

➡ particules étendues (Dirac 1962)

➡ modèles en vogue dans les années 1960 pour l’interaction forte

Chew (1961), Veneziano (1968)
difficultés expérimentales ➡ abandon en faveur de QCD

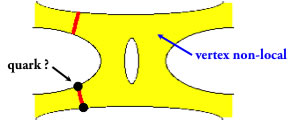
Modèle de cordes pour l'interaction forte

Scherk, Schwarz, Toneya (1974) : théorie de la gravitation ?

gravitation ⬄ échelle de Planck

Théorie des cordes

Corde ouverte

libre
- spectre de vibrations = « tour » de particules
- masse = 0, masse = M_Planck, masse = 2 M_Planck etc.
interaction : fusion/scission de cordes
et les charges électriques ?
nombres quantiques attachés aux extrémités ➡ groupes de symétrie

Corde ouverte avec des charges aux extrémités

Corde ouverte ➡ corde fermée

Corde fermée ➡ graviton de spin 2

Supercordes

Vibrations d’un corde ➡ degrés de liberté bosoniques (spins 0, 1, 2…)

Et les fermions ? ➡ supercordes

coordonnées spinorielles (anticommutantes) sur la corde
supersymétrie boson ⬄ fermion

Dans cette généralisation de l'action de Polyakov, on a introduit des coordonnées Y_m qui sont des spineurs sur la surface d'univers, mais des vecteurs à D dimensions pour l'espace temps: la partie droite rappelle l'équation de Dirac (les I^a étant les matrices de Dirac en deux dimensions)

Cettea action est invariante sous la transformation de X en Y et de Y en X (supersymétrie)

On peut également ajouter un indice de symétrie interne (et donc une symétrie de jauge) aux coordonnées X et Y, ce qui permet de décrire les interactions forte et électrofaible dans ce formalisme.

Comme toute théorie quantique des champs, celle-ci présente des "anomalies" (perte des symétries classiques lors de la renormalisation) qui, dans certains cas très particuliers, ont le bon goût de se compenser (comme dans le modèle standard des particules où les anomalies des leptons compensent celles des quarks). Mais ceci n'arrive que si

l'espace-temps est de dimension 10 = 1+9
le groupe de jauge interne est restreint à
- SO(32) Green & Schwarz (1984) : 3 modèles cohérents seulement (I, IIA et IIB)
- E(8)xE(8) Gross, Harvey, Martinec & Rohm (1985) : 2 variantes supplémentaires (dites hétérotiques)

Doit-on y voir une difficulté de la théorie ou au contraire un succès éclatant (la dimension de l'espace-temps et le ssymétries internes sont déterminées)?

➡ seulement 5 théories possibles

I cordes ouvertes, SO(32)
IIA cordes fermées non chirales
IIB cordes fermées chirales
hétérotique O cordes fermées chirales
hétérotique E cordes fermées chirales

et elles semblent des variantes d’une même « théorie M » sous-jacente ?

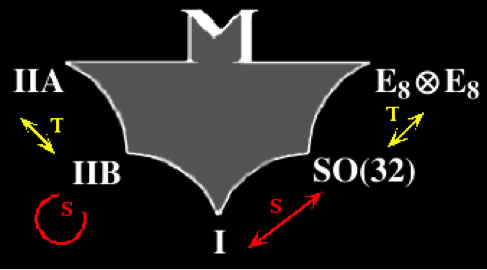
Théorie M et théories de cordes

Dualités

Dualité S : deux théories A et B sont S-duales si la limite à couplage faible de la théorie A est identique à la limite à couplage fort de la théorie B et inversement (on passe de l'une à l'autre en remplaçant g ⬄ 1/g )

Dualité T : deux théories A et B sont T-duales si la limite à courte distance de la théorie A est identique à la limite à grande distance de la théorie B et inversement (on passe de l'une à l'autre en changeant R ⬄ 1/R).

Cela vient du fait qu'une une corde enroulée autour d’une dimension compacte de rayon R a des modes de vibration proportionnels à 1/R et des modes d’enroulement (« winding ») proportionnels à R.

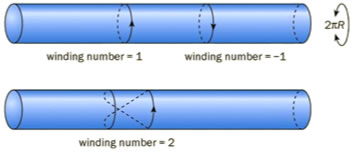
Dualité T

10 dimensions, c’est 6 de trop !

➡ rendre les 6 dimensions supplémentaires repliées sur elles-mêmes de manière compacte

➡ très nombreuses façons de le faire

sphères S6
espaces de Calabi-Yau
orbifolds

➡ ~10⁵⁰⁰ solutions possibles = « paysage » (landscape) correspondant chacune à une physique très différente

Orbifold (vision d'artiste)

Inconvénients

On aboutit à une théorie qui prévoit un espace-temps à 10 dimensions

Les conséquences physiques en 4 dimensions sont extrêmement floues (car tout semble possible), fort peu testables et présentent quelques inconvénients:

possibilité de varier la taille et la forme de l’espace compact, conduisant en 4 dimensions à la présence de champs scalaires, les « modules ».
dont l'existence entraîne physique différente selon leurs couplages, leurs masses, etc.
violation du principe d’équivalence
variation au cours du temps des constantes fondamentales
difficultés avec la cosmologie

On a aussi perdu l’interprétation géométrique de la gravitation: le principe d’équivalence est une simple coïncidence ➡ on a perdu Einstein !

Branes

Corde à 1 dimension, pourquoi pas des « branes » à 2, 3, 4… dimensions en plus des cordes ?

Objets à p dimensions, les branes, permettent la possibilité que les extrémités des cordes ouvertes soient assujetties à une p-brane

Alors les champs de matière et leurs interactions (cordes ouvertes) sont assujetties à cette p-brane, tandis que la gravitation (cordes fermées) peut se déployer dans les D dimensions de l’espace-temps total (« bulk »)

Cela expliquerait la faiblesse relative de la gravitation comparée aux autres interactions (Arkani-Hamed, Dimopoulos & Dvali 1998)

Dans cette approche, notre univers est une 4-brane plongée dans un espace-temps à 10 dimensions

les cordes ouvertes (➛ particules) sont ancrées sur la brane
les cordes fermées (➛ gravitation) se propagent en dehors

Brane et cordes

Une géométrie de Minkowski est possible sur la brane (Randall & Sundrum 1999) si on suppose une constante cosmologique négative dans le « bulk » (ce qu'on appelle un espace anti-deSitter, ou AdS), une tension constante sur la brane et l'équation d’Einstein en 5 (ou 10) dimensions. En dehors de conduire à un espace-temps plat sur la 4-brane, cette équation permet de calculer

l'évolution de la brane et du bulk
les transferts d’énergie entre la brane et le bulk

Rien n'interdit bien sûr l'existence d'autres branes dans l'espace-temps à 10 dimensions. Elles interagissent gravitationnellement, mais comme on ne les voie pas (les interactions électromagnétiques sont confinées à notre 4-brane) leur présence est interprétée comme de la matière noire et/ou de l'énergie noire.

Rien n'interdit non plus à deux branes de se croiser et même d'entrer en collision: cela pourrait être l'origine du big bang (scénario dit ekpyrotique)

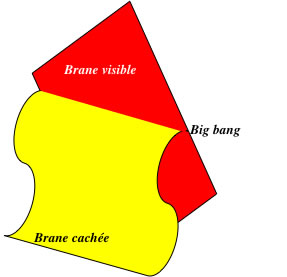
Scénario ekpyrotique

On peut retrouver la cosmologie du big bang dans ce cadre (Langlois et al.). La version simple suppose une brane à 3 dimensions spatiales dans un espace-temps à 4+1 dimensions et elle aboutit à une équation de Friedmann modifiée, équivalente en 4 dimensions à l'équation habituelle sauf à très haute énergie (paramètre d'échelle tendant vers zéro)

Pour une théorie fondamentale à 10 ou 11 dimensions, on aurait la situation suivante

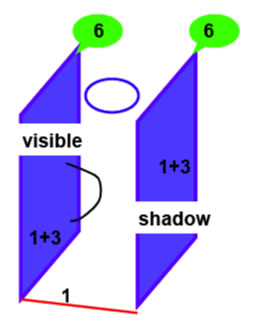
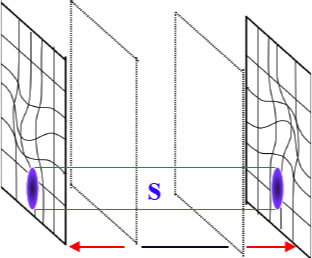
Cosmologie branaire Influences entre branes

où le sperturbations d'une brane sur sa voisine pourraient être à l'origine des fluctuations primodiales de densité censées être à l'origine des grandes structures comme les galaxies.

Contraintes expérimentales

Un autre iintérêt des branes est de rapprocher l’échelle de Planck de l’échelle électrofaible (Arkani-Hamed, Dimopoulos & Dvali 1998), ce qui permet de tester en accélérateur cette théorie

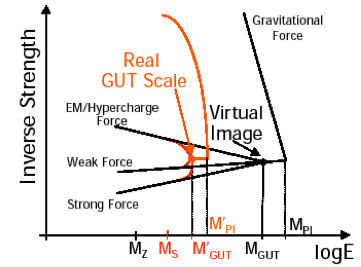
Compactification à grande échelle

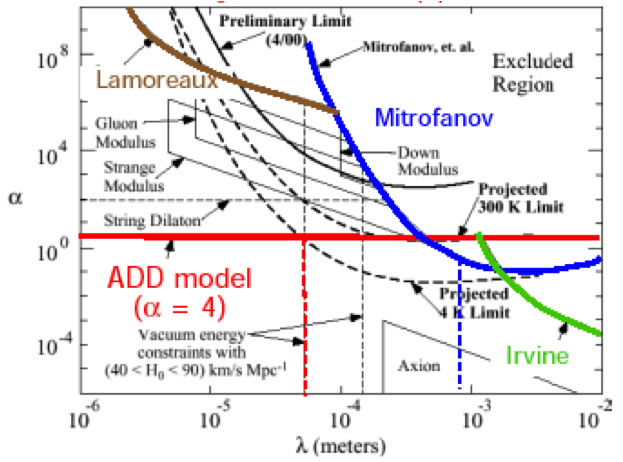
Limites au Tevatron (à mettre à jour avec le LHC)

1 dimension supplémentaire: < 0.3 mm
7 dimensions: aucune > 2x10^-15 m

Actuellement, la loi en 1/r² de Newton est bien vérifiée sur des échelles allant de 0.1 mm à 10¹⁶ m

Déviation à la loi de Newton

L'espace existe-t-il?

La théorie des cordes et des branes possède un très grave défaut : elle exige en arrière-plan un espace-temps fixe (background metric)

Deux conceptions de l’espace s’affrontent depuis Aristote et Démocrite, Newton et Leibniz :

L’espace est une scène sur laquelle se déplacent des objets et il existe indépendamment d’eux ➡ Dynamique et gravitation classiques ➡ Mécanique quantique, théorie des champs ➡ Théorie des cordes
L’espace est le réseau des relations entre des objets et il n’existe pas indépendamment d’eux ➡ Relativité générale ➡ Théorie des boucles

Boucles et réseaux de spins

Une longue histoire tourmentée

Focalisée sur la gravitation (⬄il n’est pas question d’unification avec les autres interactions) et sur l’aspect géométrique de la relativité générale

On part de la formulation hamiltonienne de la mécanique, décrite par un hamiltonien H(p,q) fonction des coordonnées généralisées q et de leurs moments conjugués p. On applique la quantification "canonique" consistant à remplacer les coordonnées q et les moments p par des opérateurs Q et P, et les crochets de Poisson {p,q} par des commutateurs [P,Q]. Ces opérateurs agissent sur des états |ψ> éléments d'un espace vectoriel)

Appliquée à la relativité générale, les coordonnées sont les éléments du tenseur métrique g

La quantification « canonique » se complique lorsque la théorie doit satisfaire des contraintes, ce qui s'exprime en général par des équations de la forme C(q) = 0. C'est notament le cas des théories qui présentent des symétries:

invariance globale de Lorentz-Poincaré
invariance locale par reparamétrisation (difféomorphisme)
invariance locale de jauge

En 1950, Dirac montra que la meilleure façon de procéder était de quantifier sans tenir compte des contraintes, puis d'exiger que les états |ψ> satisfassent à une équation C|ψ> = 0

Equation de Wheeler-DeWitt (1967)

Le point de départ est de décomposer le tenseur métrique g_mn à 4 dimensions spatio-temporelles en un tenseur à 3 dimensions spatiales h_ij et deux vecteurs décrivant le déplacement de cette surface. Dans cette décomposition due à Arnowitt, Deser et Misner (1962)'invariance globale est ainsi perdue, mais l'intérêt est que le hamiltonien ne dépend que de la 3-géométrie, et la contrainte de Dirac est juste

H|ψ> = 0

Cette équation est trompeusement simple: elle s'écrit en fait

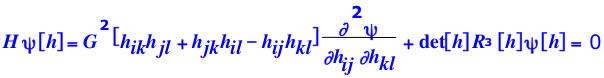
Equation de Wheeler-DeWitt

faisant apparaître la dépendance fortement non-linéaire de la fonction d'onde (de l'univers) |ψ> dans la 3-géométrie h_ij

Cette équation n’est en pratique soluble que pour des cas extrêmement simples d'un mini-superespace (univers homogène et isotrope). Dans ce cas le hamiltonien (et le lagrangien) ne dépendent que du paramètre d'échelle a, la seule variable dynamique, et de sa dérivée temporelle a' (ou du moment conjugué p = –3πaa'/2G)

Le lagrangien L = -3πa³/4G [(a’/a)² + 8πGr/3 - k/a²+ Λ/3] donne l'équation de Friedmann comme équation du mouvement. Qu'a-t-on gagné? Une version quantique de la théorie du big bang!

L'équation de Wheeler-DeWitt est en effet

{-d²/da² + 9π²/4G² [ -8πGρa⁴ + ka² - Λ a⁴/3 ] } ψ(a) = 0

qui est une équation de Schrödinger pour une particule de coordonnée a dans un potentiel V(a)

V(a) = 9π²/4G² [ -8πGρa⁴ + ka² - Λ a⁴/3 ]

Pour ρ = 0 et k = +1 (univers de de Sitter fermé) la solution classique n’existe que si a > √(3/Λ), mais il y a un effet tunnel quantique si a < √(3/Λ) que l'on peut interpréter comme une « création spontanée de l’univers »

Mais c’est à peu près tout ce qu’on sait faire ! Hawking et Hartle (1983) ont tenté d'aller plus loin, mais leurs tentatives sont restées inabouties.

Une nouvelle paramétrisation de la métrique par Ashtekar (1986) a permis, au cours des années 1990, le développement d'une nouvelle approche de la quantification de l’espace-temps par Baez, Jacobson, Rovelli, Smolin et al. Ils montrèrent que l’équation de Wheeler-DeWitt dans les variables d’Ashtekar avait des boucles comme solutions, et que les opérateurs associés à la surface et au volume avaient des valeurs propres quantifiées (ce qu'on peut interpréter comm eune quantification de l'espace-temps).

➡ développement du formalisme des réseaux de spins

Réseaux de spins

L’espace des états (de l’espace-temps) est défini à partir de graphes (réseaux) tridimensionnels

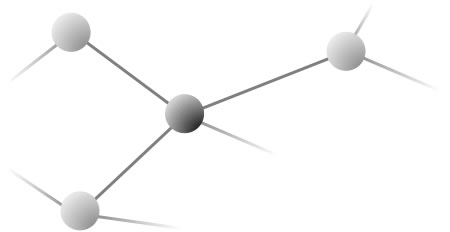Réseau de spins Réseau de "spins"

les liens portent des indices de SU(2) ⬄ « spins »

et les vertex des tenseurs de SU(2) ⬄ comment les liens se connectent

Discrétisation de l'espace

Dual du réseau de spins → cellules polyédriques

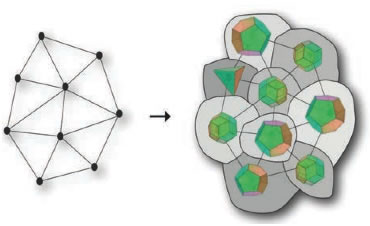
Du réseau de spins à son dual polyédrique

On peut considérer ces polyèdres comme des quanta d’espace

Ils ne sont pas dans l’espace, ils sont l’espace

Géométrie quantique

La géométrie de chaque polyèdre est définie par des paramètres (angles et surfaces) qui ne commutent pas nécessairement ⇒ inégalités du type de Heisenberg

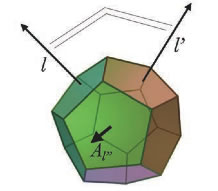Angles et surfaces d'un polyèdre élémentaire

Un état quelconque de l’espace est une superposition linéaire de différents réseaux de spin

Les opérateurs de surface et de volume ont un spectre discret

S = 8πγ ħ G/c³ [ j(j+1) ] ^½ = 8πγ L_Planck² [ j(j+1) ] ^½ où j = 0, ½ , 1 …
et Volume ~ L_Planck³

Le paramètre γ de la formule précédente est le paramètre d'Immirzi, non défini dans la théorie.

L'espace-temps

Réseau de spins = espace

Changement des connexions = temps

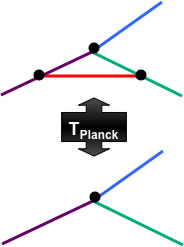Changement d'un réseau de spins = temps

Espace-temps → « mousse de spins »

Mousse de spins

Évolution ➡ amplitudes de transition d’un état à un autre

L’espace-temps est-il une cotte de mailles?

À petite échelle, l’espace-temps est une superposition quantique de boucles/mailles formant des réseaux de spin

Les mailles ont une taille finie ⇒ les amplitudes de transition sont bien définies (pas de divergence)

A grande échelle l’espace – et l’espace-temps – semblent (peut-être) continus comme un tissu (weave)

Tisser une cotte de mailles

Mais on ne sait pas si cela est toujours vrai, ou seulement dans des cas exceptionnels

Et les autres interactions n’ont rien à voir avec la gravitation

Cosmologie et gravitation quantique

Dans la théorie des boucles, il y a une « distance » minimale, la longueur de Planck

Le paramètre d’échelle a est quantifié : a_n = a₁√n

La densité d’énergie E est elle aussi quantifiée, et ne diverge pas quand n➛0

➡ Bojowald a montré qu'il n'y avait pas de singularité dans ce cas : une contraction conduit à un rebond vers une expansion

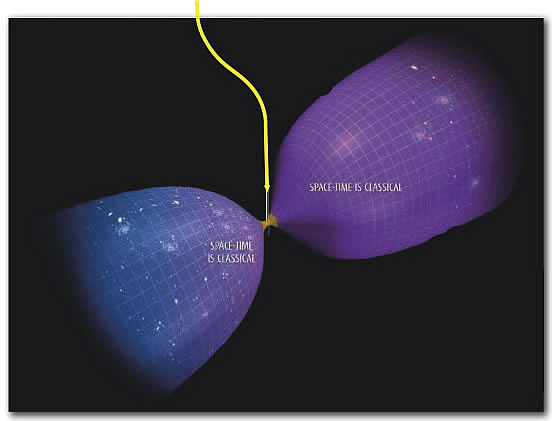
Cosmologie dans le modèle des boucles

Alternatives

collision de branes (modèle ekpyrotique)
T-dualité dans les théories de cordes entre a et 1/a (modèle de pré big bang)
etc.

En résumé

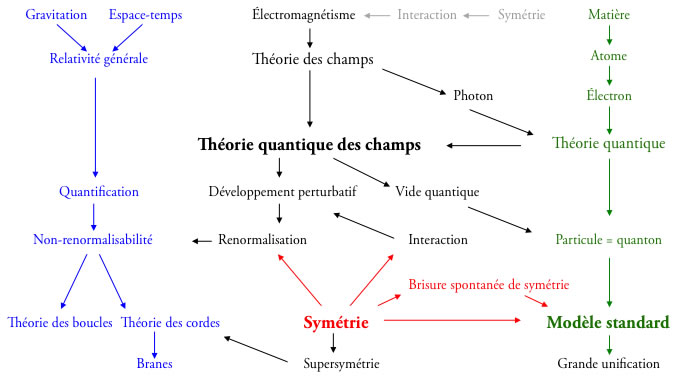
La physique des particules d'un coup d'oeil

Et tout ce dont on n'a pas parlé

Patience du chat

L’être et le néant

pourquoi y a-t-il quelque chose plutôt que rien ?

la création du monde est-elle inévitable ?

la réponse est 42, mais quelle est la question ?

L’irréversibilité du temps

pourquoi ne peut-on pas faire d’œufs avec des omelettes ?

Les paradoxes quantiques

il n’y a pas que le chat de Schrödinger !

Livre de Schrödinger: Physique quantique et représentation du monde

L’élégance en science

la beauté est dans l’œil de celui qui regarde (☛ motivation de Platon à Dirac)

mais elle est un guide trompeur : les planètes ne décrivent pas des cercles mais des trajectoires très complexes

Le difficile combat de Johannes Kepler, vu par Sidney Harris

Le modèle standard n’est pas très élégant, et probablement incomplet, comment aller au-delà ?

Contact