Alain Bouquet - Vers la théorie quantique

Dans son modèle, par simplicité, Bohr avait supposé que les électrons suivaient des trajectoires circulaires. Le moment angulaire d'un électron en rotation est un vecteur L, de norme |L| et pointant dans la direction perpendiculaire au plan de rotation. La condition de Bohr quantification du moment angulaire (L=nħ) se décomposait en fait en deux parties:

une quantification de la norme |L| du moment angulaire lui-même ➛ nombre quantique n
une quantification de la projection de ce moment angulaire sur un axe a priori arbitraire ➛ nombre quantique m (variant de -n à +n)

L'énergie de chaque orbite (E_n=E₀/n²) étant déterminée par le nombre quantique n indépendamment de la valeur de m, celui-ci reçut peu d'attention initialement. Mais il perturbait les théoriciens, car ils ne comprenaient pas comment la projection du moment angulaire sur un axe arbitraire pouvait être quantifiée sans remette en question l'invariance par rotation. Cela paraissait impliquer l'existence de directions privilégiées dans l'espace (celles dans lesquelles le moment angulaire était quantifié) et la notion de "quantification de l'espace" fut dans l'air pendant une quinzaine d'années. L'expérience de Stern et Gerlach (cf. infra) fut explicitement conçue pour démontrer cette "quantification de l'espace". La mécanique quantique résolut le dilemme en conservant la symétrie de rotation et en montrant que les états quantiques dont la projection du moment angulaire dans une direction donnée est définie sont des superpositions quantiques d'états de projection donnée dans d'autres directions. On ne parle plus de quantification de l'espace mais de quantification du moment angulaire.

Niveaux d'énergie de l'atome d'hydrogène

Niveaux d'énergie de l'hydrogène

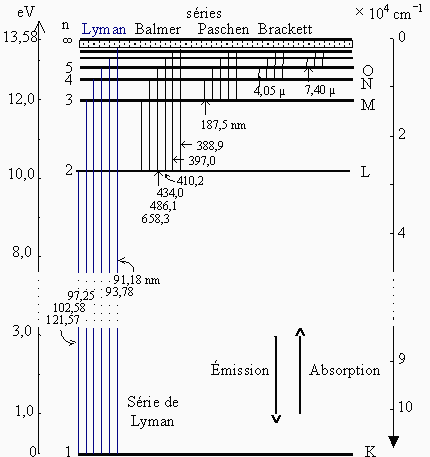
Principe de correspondance (1913)

Expérience de Franck et Hertz (1914)

James Franck (1882-1964) et Gustav Hertz (1887-1975), le neveu de Heinrich Hertz, réalisèrent en 1914 une expérience qui démontrait l'existence des niveaux d'énergie de l'atome de Bohr même en l'absence de rayonnement. L'expérience utilisait une triode remplie de vapeur de mercure à une pression ~0.1 Pa (10^–6 atmosphères). Des électrons émis par une cathode, accélérés par une grille, entraient en collision avec les atomes du gaz et perdaient alors de l'énergie. Les électrons ralentis traversaient la grille, qui les freinait encore. Une anode collectrice à un potentiel un peu plus bas (0.5 V) que la grille récupérait les électrons. Une perte d'énergie importante des électrons au cours des collisions les rendaient incapables d'atteindre l'anode (ils rejoignaient alors la grille), ce qui se traduisait par une chute du courant dans la seconde partie du tube.

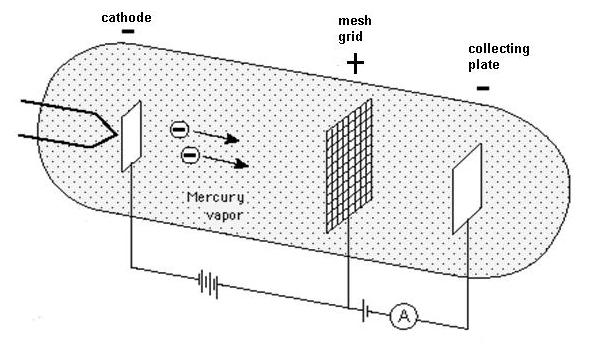
Expérience de Franck et Hertz

Schéma de l'expérience de Franck et Hertz

Le but de l'expérience était de démontrer que lorsque la tension appliquée à la grille atteint certaines valeurs précises, l'énergie de l'électron devient juste suffisante pour induire des transitions dans les atomes de mercure. La collision devient inélastique, l'électron incident cède son énergie à l'atome, et il n'a plus l'énergie suffisante pour atteindre l'anode. Le courant chute alors brutalement. Puis il remonte quand la tension de la grille augmente, jusqu'à atteindre l'énergie suffisante pour exciter deux atomes de mercure. Le courant retombe alors puis remonte jusqu'à 14.7 V, et retombe à nouveau.

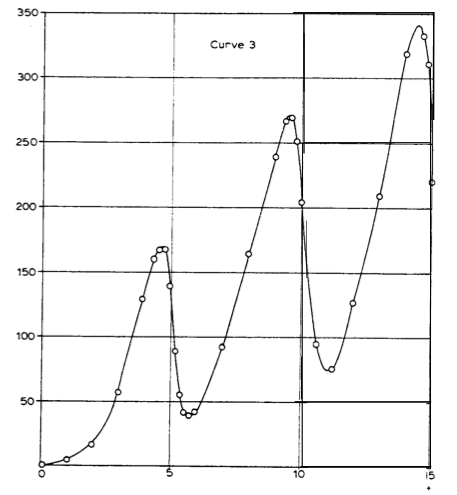
Résultats de l'expérience de Franck et Hertz

Résultat de l'expérience de Franck et Hertz (Franck, conférence Nobel 1925): chaque fois qu'un électron atteint une énergie de 4.9 eV (voltage de 4.9 V), il excite un atome de mercure. Quand il atteint 2*4.9=9.8 eV, il en excite 2, quand il atteint 3*4.9=14.7 eV, il en excite 3, et ainsi de suite (jusqu'à une tension voisine de 100 V). La valeur de 4.9 eV observée dans le cas du mercure correspond (via E=hν=hc/λ) à une longueur d'onde de 254 nm, qui correspond bien à une raie intense dans le spectre d'émission du mercure (dans l'ultraviolet).

Franck

Franck et Hertz reçurent en récompense le prix Nobel de physique en 1925, puis leurs destinées furent bien différentes. James Frank fut professeur à Göttingen et directeur de l'Institut de Physique Expérimentale, position parallèle à celle qu'avait Max Born du côté de la théorie. D'origine juive, Franck quitta son poste, et l'Allemagne, en 1933 pour les États-Unis. Professeur à Baltimore puis, après une année à Copenhague, à Chicago, il y devint un des éléments clés du programme Manhattan, en charge de superviser la chimie de l'uranium et du plutonium. Profondément intéressé par les aspects politiques et éthiques des armes nucléaires, il fut le coordinateur du rapport Frank en juin 1945 déconseillant l'emploi de ces armes contre les villes du Japon.

Gustav Hertz, dont l'un des grand-pères était juif, perdit son poste universitaire à Berlin et devint directeur de la recherche chez Siemens jusqu'en 1945. En 1945, avec plus d'une centaine d'autres physiciens allemands (dont Manfred von Ardenne, Peter Thiessen ou Heinz Barwich), il rejoignit l'Union Soviétique où il dirigea les recherches sur la séparation isotopique par diffusion gazeuse (domaine sur lequel il travaillait depuis 1928) près de Soukhoumi en Géorgie sur la Mer Noire. Il reçut un Prix Staline en 1951, puis il put rejoindre Leipzig en 1955 mais il demeura en RDA jusqu'à sa mort.

Timbre à l'effigie de Hertz

Timbre de l'Allemagne de l'Est à l'effigie de Gustav Hertz, rendant hommage à ses travaux sur la séparation isotopique de l'uranium

Le modèle de Bohr-Sommerfeld

Dans ses articles de 1913, Bohr n'avait supposé que des orbites circulaires et Peter Debye suggéra immédiatement la possibilité d'orbites elliptiques. Cela paraissait logique: le mouvement fermé d'une masse soumise à une force en 1/r² est en général une ellipse, dont le cercle est un cas très particulier. Le calcul n'était pas beaucoup plus complexe que celui de Bohr, il fallait juste tenir compte de la variation périodique de la distance radiale r.

Cela introduisait un nouveau nombre quantique k (>0) et l'énergie d'un électron sur une orbite de nombres quantiques {n,k} devenait

E_n=E₀/(n+k)²

On retrouvait donc la formule de Bohr, mais avec n+k au lieu de n. Pour éviter toute confusion, il est préférable d'effectuer les substitutions n➛l puis l+k➛n. Alors:

E_n=E₀/n²

l ≤ n (puisque k > 0) et -l < m < l

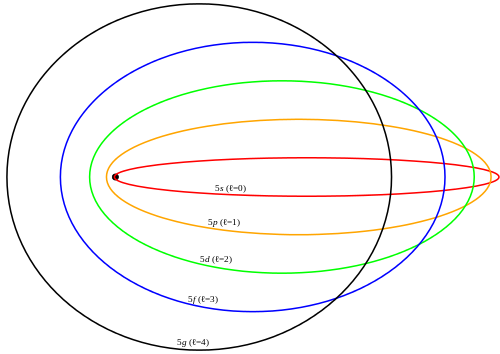
Ellipses de Sommerfeld

Ellipses de Sommerfeld pour n=5 (et l=0, 1, 2, 3 et 4). 3° loi de Kepler ➛ même période orbitale pour même ½ grand axe (quelle que soit l’ellipticité).

½ grand axe a(n,l) = R₀n² ne dépend pas de l ☛ « dégénérescence »
½ petit axe b(n,l) = R₀nl
énergie E(n,l) = E₀/n² en 1° approximation

Sommerfeld tint ensuite compte des corrections relativistes. Elles seraient faibles, car la vitesse v de l'électron dans un atome était estimée très inférieure à la vitesse c de la lumière (en utilisant v/c ~ √(2E/mc² ➛v/c<1%), mais le but de Sommerfeld était de rendre compte de la structure fine du spectre de l'hydrogène.

La structure fine

La formule de Balmer-Rydberg, utilisée par Bohr dans la construction de son modèle en 1913, n'était pas tout à fait correcte car elle négligeait le fait que chacune des raies apparaissaient sous une meilleure résolution comme une série de raies étroites très proches: la "structure fine". Michelson fut le premier à en signaler la présence en 1892, ce que des expériences ultérieures confirmèrent.

Structure fine de H alpha

La structure fine de la raie H_α de l'hydrogène

Bohr avait suggéré en 1914 que les corrections relativistes à la masse de l'électron (plus exactement à la relation entre masse, vitesse, énergie et impulsion) pourraient expliquer la structure fine, mais sans mener le calcul à son terme. Au cours de l'hiver 1914-1915, Arnold Sommerfeld se lança dans le calcul des corrections relativistes pour aboutir en janvier 1916 à une formule un peu plus complexe que celle de Rydberg:

E_nk = E₀ [Z²/n² + α² Z⁴/n³ (1/k - 3/4n) ] + O(α⁴)

Le premier terme de la formule généralisée redonnait le résultat de Bohr (et donc la formule de Rydberg) et le second était numériquement une petite correction. Dans son calcul, Sommerfeld avait introduit une notation α=2πe²/hc qui resta ensuite sous le nom de "constante de structure fine" et qui est nombre pur, sans dimension, et dont la valeur (~1/137) est petite devant 1. Les termes en α² sont donc négligeables en première approximation, et ceux en α⁴ plus encore.

En première approximation, l'énergie de l'électron ne dépendait pas séparément des nombres quantiques k et l mais seulement de leur somme n=k+l. Les effets relativistes "levaient la dégénérescence" et différenciaient l'énergie de l'électron selon l'ellipticité et l'orientation de son orbite, d'où la structure fine.

Mais l'amélioration de la spectroscopie, par Paschen en particulier, montra que l'on n'observait pas toutes les transitions a priori possibles d'un niveau (n,k) vers un niveau (n',k'). Il existait manifestement des règles de sélection. Certaines n'apparaissaient qu'en présence d'un champ magnétique ou électrique (effets Zeeman et Stark), d'autres n'apparaissaient pas du tout. Apparemment il fallait que k'=k±1. Mais pas toujours. Une issue à ces difficultés fut proposée en août 1925 par George Uhlenbeck et Samuel Goudsmit à Leyde: remplacer k par j+½ et limiter les transitions à celles où j'=j ou bien j'=j±1. Uhlenbeck et Goudsmit ne justifiaient pas leur règle, mais elle les conduisit en octobre 1925 à proposer la notion de spin de l'électron. La quantité j représente alors le moment angulaire total d'un électron (spin + moment orbital) et leur règle de sélection est due au fait que le spin du photon est 1.

Incidemment, la précision des mesures a longtemps laissé penser que la constante de structure fine α pourrait être (l'inverse d') un nombre entier, 1/136 puis 1/137, ce qui suscita une effervescence de "dérivations" numérologiques, en particulier par le grand astrophysicien Arthur Stanley Eddington. Ces spéculations furent parodiées en 1931 par Hans Bethe, avec la complicité de Guido Beck et Wolfgang Riezler dans un article qui fut publié, sans sourciller, par la très sérieuse revue Naturwissenschaften: les auteurs considéraient un cristal à la température du zéro absolu (T₀=-273°C), attribuaient un nombre de degrés de liberté égal à 1/α aux électrons comme aux protons (suivant en cela la proposition d'Eddington) et en déduisaient que pour arriver au zéro absolu il fallait retirer tous les degrés de liberté (sauf un "en raison du mouvement orbital"), d'où T₀=-(2/α–1)=-273 ⇔ α=1/137! La dérivation de Bethe et ses complices est bien sûr totalement loufoque et digne d'Alan Sokal. Naturwissenschaften publia un "erratum" en 1932 pour s'excuser. La valeur actuelle de la constante de structure fine est α=1/137.036…

Sommerfeld

Arnold Sommerfeld (1868-1951)

Sommerfeld est une figure étonnante de la physique. Aucun physicien ne fut aussi souvent proposé pour le prix Nobel (81 fois), mais il ne le reçut jamais. Par contre, la liste de ses élèves est un florilège de la physique de la première moitié du 20° siècle, sept d'entre eux recevant un prix Nobel: Werner Heisenberg, Wolfgang Pauli, Peter Debye, Hans Bethe, Max von Laue, Isidore Isaac Rabi, Linus Pauling. Parmi ses élèves figuraient aussi Paul Peter Ewald, Herbert Fröhlich, Ludwig Hopf, Alfred Landé, Rudolf Peierls, Gregor Wentzel, Linus Pauling, Walter Heitler et bien d'autres.

Né à Königsberg, Sommerfeld y fit ses études (ayant entre autres professeurs Hilbert et Wiechert) avant d'aller à Göttingen où il fut l'assistant du mathématicien Felix Klein. Il devint assistant-professeur de mathématiques (Privatdozent) à Göttingen en 1895, professeur de mécanique à Aix-la-Chapelle en 1900 où il développa l'hydrodynamique, puis en 1906 professeur à Munich et directeur du nouvel Institut de Physique Théorique. En 1911, Sommerfeld nota que la constante de Planck h avait pour dimension énergie*temps, la même que l'action (celle que l'on minimise dans le principe de moindre action qui est à la base de la mécanique lagrangienne ou hamiltonienne) et il avait cherché à relier le "quantum d'action" h à la quantification de l'action d'un système physique. Après la publication du modèle de Bohr, il le généralisa en imposant en 1916 la quantification pour chaque degré de liberté q sous la forme ∲pdq=nħ (p étant le moment conjugué à q). En 1918, il devint président de la Société allemande de physique, et il lança en 1920 une nouvelle revue, le Zeitschrift für Physik, qui devint immédiatement une des revues majeures du domaine au niveau mondial. Sommerfeld prit sa retraite en 1935, mais resta en poste jusqu'à la guerre, faute de successeur. Ses traités de 1919 Atombau und Spektrallienien et de 1929 Wellenmechanische Ergänzungsband furent successivement les "bibles" de la physique atomique pour deux générations de physiciens.

Dans le modèle de Bohr-Sommerfeld, la position d'un électron en 3 dimensions conduisait automatiquement à trois nombres quantiques (n, l et m) en généralisant la règle de quantification de Bohr qui s'appliquait au mouvement à une dimension de l'électron autour d'une orbite circulaire fixée.

n = 1, 2, 3…
l = 0, 1,… n-1
m = -l, -l+1… l-1, l

Ces règles viennent de ce que la position d'un électron est donnée en coordonnées sphérique par trois variables (r, θ, φ), que la quantification porte sur les moments conjugués (variable q ➛ moment conjugué p=∂L/∂q où L est le lagrangien) sous la forme ∲pdq=nħ ☞ 3 nombres quantiques n_r, n_θ et n_φ que l'on regroupe sous la forme

n = n_r + n_θ + n_φ
l = n_θ + n_φ– 1
m = n_φ

Mais l'énergie d'une orbite ne dépendait en première approximation que du nombre quantique n, en deuxième approximation des nombres n et l, et en troisième approximation des trois nombres séparément (levées de dégénérescence, en présence de champs électriques ou magnétiques externes par exemple, ou de corrections relativistes). Un quatrième nombre quantique, le spin avec deux valeurs possibles, fut ensuite ajouté pour déterminer complètement l'état d'un électron.

Lewis et Langmuir

Modèle en couches et liaisons chimiques (1916)

Stern et Gerlach

Le modèle de Bohr-Sommerfeld supposait que les orbites des électrons étaient quantifiées: les rayons ne pouvaient avoir que certaines valeurs, de même que l'orientation des plans orbitaux. Ceci est une conséquence de la quantification du moment angulaire. Pour le démontrer, une expérience fut imaginée en 1921 par Otto Stern, professeur à Rostock et ancien assistant de Max Born, (Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld "Une méthode pour démontrer expérimentalement la quantification de la direction avec un champ magnétique"). Il la réalisa l'année suivante avec Walther Gerlach, professeur de physique expérimentale à Francfort/Main (Das magnetische Moment des Silberatoms).

L'idée de départ de Stern était qu'un atome, parce qu'il possédait des charges électriques (les électrons) en rotation devait se comporter comme un aimant miniature dont les pôles seraient déterminés par le plan de rotation (et le sens de rotation) des électrons. Si dans la théorie classique de Larmor, les pôles n'avaient pas de direction privilégiée, ils en avaient dans celle de Sommerfeld.

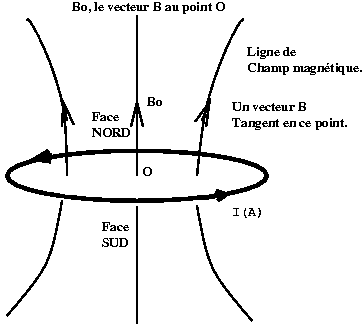
Champ créé par une spire

Champ magnétique créé par une boucle de courant

Des aimants (un dipôle magnétique) placé dans un champ magnétique homogène subit un couple qui l'aligne sur le champ, mais cela ne déplace pas son centre de gravité. Stern suggéra de placer ces atomes dans un champ magnétique non homogène (avec un gradient selon une direction, verticale par exemple). Dans ce cas un aimant non seulement tourne sur lui-même mais il se déplace également dans la direction du gradient (ou la direction opposée selon son orientation). Si les atomes se déplacent perpendiculairement au champ (parce qu'ils appartiennent à un jet atomique par exemple), ils vont arriver sur un écran à une position plus ou moins haute, selon l'orientation initiale de leur moment magnétique. La théorie classique prédit donc qu'ils vont arriver le long d'une ligne d'impacts, la théorie quantique qu'ils vont arriver sur à des positions discrètes (mais alignées sur la verticale).

Les atomes sont a priori dans leur état de plus basse énergie (nombre quantique n=1) et dans la théorie de Bohr-Sommerfeld, le moment angulaire ne peut avoir que deux valeurs L=±1. Un jet d'atomes devrait donc donner deux impacts distincts, selon que le moment angulaire (et donc le moment magnétique) est parallèle (L=+1) ou antiparallèle (L=–1) avec le champ magnétique.

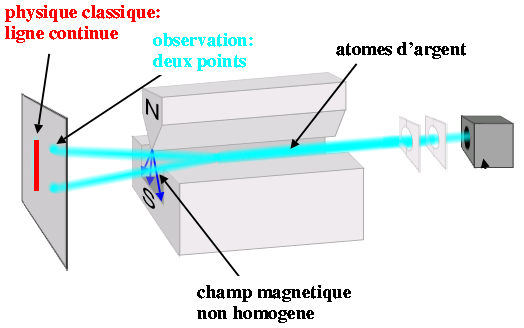
Expérience de Stern et Gerlach

Expérience de Stern et Gerlach (Wikipedia)

Stern calcula que, pour que les impacts soient bien séparés, il faudrait un gradient de champ magnétique de 1 tesla par cm et il demanda à Gerlach si cela était réalisable. Gerlach répondit que cela ne posait aucun problème. Ils utilisèrent un jet d'atomes d'argents, vaporisés dans un four à 1000°C, sortant par deux étroites ouvertures de 0.03 mm (formant un collimateur) à une vitesse ~700 m/s et traversant un aimant de 3.5 cm de long qui créait un champ de 0.1 T avec un gradient de 10 T/cm. L'expérience étrait très délicate: le collimateur et l'aimant devaient être alignés avec une précision extrême, le dépôt d'argent était très faible et donc difficile à mettre en évidence. Stern attribua par la suite la réussite de l'expérience aux mauvais cigares qu'ils fumaient: chargée en soufre, leur fumée noircissait l'argent et facilitait involontairement l'observation. De plus, la situation financière de l'Allemagne était alors critique, et seules des conférences (payantes) de Max Born, puis une aide importante de Henry Goldman (le fils du fondateur de Goldman-Sachs), permit de financer l'expérience. Stern et Gerlach faillirent abandonner à plusieurs reprises mais finalement, en février 1922, ils observèrent deux impacts distincts, séparés de 0.2 mm.

L'expérience fut donc considérée comme un succès, confirmant les idées de Sommerfeld sur la quantification du moment angulaire, et apportant une grande renommée à ses auteurs. Walther Gerlach (1889-1979) devint ensuite professeur à Tübingen puis il succéda à Wien à Munich de 1929 à 1945, puis de 1948 à 1957. La dernière année de la Seconde guerre mondiale, Gerlach fut nommé directeur du programme nucléaire allemand, et à ce titre fut interné plusieurs mois en Grande-Bretagne avec neuf autres physiciens allemands. De son côté, Otto Stern (1888-1969) devint professeur à Hambourg en 1923, poste qu'il quitta en 1933 à l'arrivée des nazis. Il partit aux États-Unis, d'abord à l'Institut Carnegie puis à l'université de Berkeley. Il reçut le prix Nobel de physique en 1943 pour ses nombreuses contributions en particulier les techniques de jets atomiques ou moléculaires, dont il était devenu le grand spécialiste, et la découverte du moment magnétique du proton et du neutron en 1933 (dont la valeur anormale suggérait que proton et neutrons n'étaient pas des particules élémentaires). Mais son expérience avec Gerlach n'était pas mentionnée par le comité Nobel, du fait des activités de Gerlach à cette époque.

En fait, l'expérience était correcte, mais son interprétation se révéla complètement erronnée. Les atomes d'argent utilisés par Stern et Gerlach ont en réalité un moment angulaire L=0 et ils auraient donc dû ne former qu'un seul point d'impact. Et s'ils avaient eu un moment angulaire |L|=1, la mécanique quantique (après les travaux de Heisenberg, Schrödinger et consorts) indiquait qu'il y aurait eu trois points d'impact et non deux! La bonne explication vint après qu'Uhlenbeck et Goudsmit eurent proposé en 1925 que les électrons possèdent un moment angulaire intrinsèque, le spin, indépendamment de leur moment angulaire orbital. L'idée de spin avait des motivations toutes différentes, mais Fraser démontra en 1927 qu'un spin 1/2 pour l'électron conduit bien à la prédiction de deux points d'impact (l'un pour un spin +1/2, l'autre pour un spin –1/2) dans l'expérience de Stern et Gerlach.

D'un autre côté, la technique utilisée par Stern et Gerlach pour séparer des états quantiques distincts fut réutilisée dans nombre de situations allant de la résonance magnétique nucléaire (RMN) au pompage optique (à la base des masers et lasers) et aux horloges atomiques.

Le spin

L'effet Zeeman anomal

L'effet Zeeman est la séparation des raies d'un spectre en présence d'un champ magnétique. Lors de sa découverte en 1896 par Pieter Zeeman, il apparut d'abord comme un élargissement de la raie, par manque de résolution. Lorentz en donna une explication en utilisant l'électromagnétisme classique qui prévoyait que la raie d'origine devait se diviser en trois raies (et plus généralement en un nombre impair de raies). Une meilleure résolution spectroscopique permit rapidement de le vérifier, mais aussi d'observer des séparations en un nombre pair de raies: cela fut qualifié d'effet Zeeman anomal (parfois écrit anormal). En fait, l'effet anomal est plus courant que l'effet normal, mais il n'est pas explicable dans la théorie de Lorentz, ni dans celle de Bohr-Sommerfeld qui conduit toujours à une séparation en un nombre impair de niveaux, et donc un nombre impair de raies (singulet, triplet ou quintuplet en général). Pour une valeur donnée de l, il y a en effet 2l+1 valeurs possibles de m (de -l à +l), ce qui est toujours un nombre impair pour l entier.

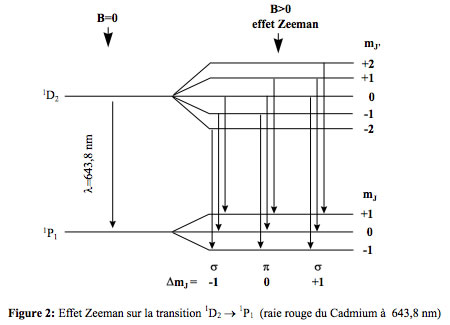
Effet Zeeman normal pour le cadmium

Deux niveaux de l'atome de cadmium séparés en 3 (l=1) et 5 (l=2) sous-niveaux par un champ magnétique: la raie de la transition, elle, est séparée en 3 composantes.

Sommerfeld et Landé avaient tenté pendant des années de trouver une explication à l'effet Zeeman anomal. Pauli se focalisa sur le cas des métaux alcalins (par exemple le doublet du sodium) qui ont un seul électron de valence, et il considéra que cet électron était le seul responsable du moment angulaire total (les "couches fermées", selon le vocabulaire de l'époque, ayant donc un moment angulaire total nul). Il finit en décembre 1924 par attribuer le doublet à eine klassisch nicht beschreibbare Art von Zweideutigkeit, "une double valeur indescriptible classiquement" de l'électron. Ralph Kronig lui suggéra que cela pourrait être une rotation de l'électron sur lui-même, avec deux sens possibles, l'idée même suggérée peu après par Uhlenbeck et Goudsmit, mais l'idée ne plut pas à Pauli car une rotation, classiquement, conduit à un moment angulaire L entier (en unités ħ) et le nombre de niveaux d'énergie 2L+1 est donc impair. Pour avoir 2 niveaux, il faut L=1/2 ce qui est, classiquement, impossible.

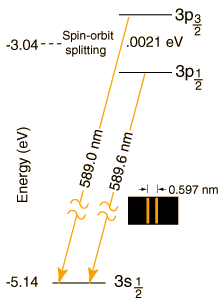
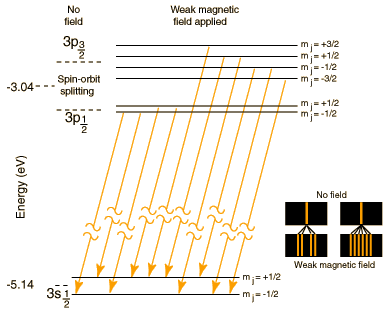
Doublet du sodium Doublet du sodium Effet Zeeman

Le doublet du sodium (dû au couplage du spin avec le champ magnétique interne engendré par le mouvement de l'électron, dit "spin-orbite"), et sa séparation en 4 et 6 sous-niveaux par un champ magnétique externe (effet Zeeman)

Introduction du spin

Uhlenbeck et Goudsmit (1925) et le spin de l'électron (Uhlenbeck, G. E. & Goudsmit, S. A. Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons. Naturwiss. 13, 953–954, 1925)

Le principe d'exclusion de Pauli

Wolfgang Pauli

Pauli Wolfgang Pauli (1900-1958) fit ses études à Vienne où il fut un étudiant extrêmement brillant. Étudiant de Sommerfeld à Munich à partir de 1918, ses premiers travaux portèrent sur le relativité générale et sur l'unification que Hermann Weyl tentait alors avec l'électromgnétisme (la théorie de Weyl est un lointain précusrseur des actuelles théories de jauge, dont le nom est d'ailleurs dû à Weyl). Sommerfeld demanda à Pauli de rédiger la partie Relativitätstheorie (Théorie de la Relativité) du tome 5 (Physique) de l'Encyklopädie der mathematischen Wissenschaften, qui apparut en 1921 sous la forme d'un texte de revue de 237 pages suscitant la profonde admiration d'Einstein. La même année, il soutint sa thèse sur la molécule d'hydrogène ionisée (l'ion H₂⁺) dans le cadre de la théorie quantique de Bohr-Sommerfeld (il conclut à son instabilité, contrairement aux observations). Pauli devint ensuite l'assistant de Max Born à Göttingen, puis de Niels Bohr à Copenhague, avant d'enseigner à Hambourg de 1923 à 1928.

C'est là qu'il proposa en 1925 le principe d'exclusion pour expliquer la structure électronique des atomes, ainsi qu'un nombre quantique additionnel (identifié au spin de Uhlenbeck et Goudsmit). En 1926, il fut le premier à appliquer la mécanique des matrices de Heisenberg à l'atome d'hydrogène.

Pauli devint professeur de physique théorique à l'ETH (École polytechnique fédérale) de Zürich en 1928, poste qu'il conserva jusqu'à la fin de sa vie. Cependant, de 1935 à 1946 il résida aux États-Unis (professeur inviité à Princeton, à l'université du Michigan et à l'université Purdue) dont il prit la nationalité en 1946 (il prit la nationalité suisse en 1949). En 1930, Pauli suggéra (dans une lettre adressée à "Chères dames et messieurs radioactifs…") l'existence d'une particule sans charge électrique et (quasiment) sans masse pour expliquer le spectre d'énergie continu des électrons dans la transmutation bêta. Ce "neutron", rebaptisé "neutrino" en 1932, ne fut expérimentalement découvert qu'en 1956 par Reines et Cowan. Pauli donna aussi en 1940 une des premières démonstrations du théorème spin-statistique, selon lequel toute particule de spin entier suit la statistique de Bose-Einstein (boson) et toute particule de spin demi-entier suit la statistique de Fermi-Dirac (fermion). Les électrons sont donc des fermions, ce qui entraîne le principe d'exclusion. En 1955, Pauli démontra aussi que, sous des conditions très générales, toute théorie théorie quantique des champs était invariante par renversement simultané du temps (symétrie T), de l'espace (symétrie P) et de la conjugaison de charge (symétrie C): c'est le "théorème CPT".

Pauli reçut en 1945 le prix Nobel de physique pour sa découverte du principe d'exclusion. Il eut comme assistants Ralph Kronig, Felix Bloch, Rudolf Peierls, Hendrik Casimir, Markus Fierz, Nicholas Kemmer, Victor Weisskopf, Res Jost. J. Robert Oppenheimer fut également son élève.

Pauli collabora également de nombreuses années avec le psychiatre Carl Gustav Jung sur les relations entre psyché et matière et le concept de "synchronicité". Pauli est également resté célèbre pour son esprit caustique (Das ist nicht nur nicht richtig, es ist nicht einmal falsch! "Non seulement ce n'est pas juste, ce n'est même pas faux!") et pour sa maladresse expérimentale (le nom "d'effet Pauli" est resté pour désigner toute catastrophe apparemment due à la seule présence de Pauli dans les environs).

Pauli et Bohr

Wolfgang Pauli et Niels Bohr à Lund (Suède) en 1954 admirant une toupie

Principe d'exclusion

Pourquoi les propriétés chimiques des éléments (le tableau de Mendeleiev) se répétaient-elles après 2, 8, 8, 18, 18 et 32 éléments? Rydberg avait remarqué que ces nombres sont de la forme 2n², où n est un nombre entier. Sommerfeld avait tenté de relier 8 aux nombres de sommets d'un cube (ce qui rappelle les efforts de Kepler pour relier les rayons des orbites des planètes aux solides platoniciens). Bohr avait essayé d'expliquer la périodicité des propriétés chimiques par le remplissage des couches successives, mais il buta sur un problème apparemment insoluble: pourquoi tous les électrons d'un atome n'étaient-ils pas sur le niveau d'énergie minimale (le fondamental)?

Tableau périodique

Dans le modèle de Bohr-Sommerfeld, les états que pouvait occuper un électron étaient caractérisés par 3 nombres quantiques (n, k ou l, et m) avec les valeurs possibles:

n =1, 2, 3…
l < n . Les valeurs l=0, 1, 2, 3, 4... sont désignées par des lettres (s, p, d, f, g) qui viennent du vocabulaire des spectroscopistes (sharp, principal, diffuse, fine…)
-l ≤ m ≤ l

Mais le modèle de Bohr-Sommerfeld restait flou sur la manière de répartir les électrons d'un atome donné sur les différentes couches, et sur la question de savoir lesquelles devaient être complètes. À l'automne 1924, Stoner publia un article s'efforçant d'améliorer ces répartitions en attribuant 2(2l+1) électrons à chaque sous-couche fermée l d'une couche n (avec l<n). Stoner posait aussi la question de savoir comment les niveaux d'énergie de l'électron de valence des atomes alcalins étaient reliés aux niveaux d'énergie des atomes des gaz nobles qui les précédaient dans le tableau périodique (He pour Li, Ne pour Na, Ar pour kr, etc.).

Il ne faut pas oublier que les physiciens de l'époque n'avaient que la périodicité des propriétés chimiques et les raies spectrales pour guides, et le modèle de Bohr-Sommerfeld comme cadre théorique.

Partant de son analyse de l'effet Zeeman anomal des atomes alcalins, Pauli l'étendit aux atomes "compliqués" en utilisant le "principe de permanence" avancé par Bohr en 1923 (Aufbauprinzip), principe affirmant que l'ajout d'un électron à un atome partiellement ionisé ne modifiait pas les nombres quantiques des électrons déjà présents. L'étendre d'un atome donné à un autre atome (de Z différent) était un saut audacieux, mais Pauli vérifia qu'il retrouvait ainsi les bonnes séparations par effet Zeeman de plusieurs atomes (le néon en particulier).

Pauli réalisa en décembre 1924 qu'il pouvait reconstituer le tableau périodique en supposant qu'il ne pouvait jamais y avoir plus de deux électrons partageant les mêmes nombres quantiques n, l et m. Il en faut deux car:

n = 1 ⇒ l = 0 ⇒ m = 0 ⇒ 1 place
n = 2 ⇒ l = 0 ou 1 ⇒ m = 0 ou m = -1, 0, 1 ⇒ 1+3 = 4 places
n = 3 ⇒ l = 0 ou 1 ou 2 ⇒ m = 0 ou m = -1, 0, 1 ou m = -2, -1, 0, 1, 2 ⇒ 1+3 + 5 = 9 places

Cela nécessitait donc qu'il puisse y avoir 2 électrons sur la première couche, 8 sur la seconde… ☛ Pauli retrouvait "la double valeur indescriptible classiquement", un nouveau nombre quantique j pouvant prendre deux valeurs, et deux seulement.

☛ Le principe "d'exclusion" (W. Pauli, “Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren”, Sur le lien entre le remplissage des groupes électroniques dans les atomes et la structure complexe des spectres, Z. Phys. 31-765-1925) est aujourd'hui formulé ainsi: un seul électron peut avoir les 4 nombres quantiques n, l, m et j.

En fait ce n'est pas si simple et le principe de Pauli ne suffit pas à lui seul à rendre compte des propriétés chimiques des atomes. En effet l'ordre de remplissage est :

1s(2 électrons) ➛ 2s(2) ➛ 2p(6) ➛ 3s(2) ➛ 3p(6) ➛ 4s(2) ➛ 3d(10) ➛ 4p(6) ➛ 5s(2) ➛ 4d(10) ➛ …

La couche 4s (n=4, l=0) se remplit avant la couche 3d (n=3, l= 2), car les niveaux d'énergie se croisent (règle empirique de Klechkowski-Madelung). Cela induit une grande similarité des propriétés physico-chimiques (dues aux électrons périphériques) des éléments situés au milieu des 4°, 5°, et 6° rang du tableau périodique (les métaux de transition). Cela se complique encore ensuite aux 6° et 7° rang où des couches profondes se complètent après les couches superficielles, ce qui conduit à la quasi-identité des propriétés chiimiques de la série des lanthanides et de la série des actinides.

Rang 1 : 2 éléments Z = 1 (H) et 2 (He)
Rang 2 : 8 éléments Z = 3 (Li) à 10 (Ne)
Rang 3 : 8 éléments Z = 11 (Na) à 18 (Ar)
Rang 4 : 18 éléments Z = 19 (K) à 36 (Kr)
Rang 5 : 18 éléments Z = 37 (Rb) à 54 (Xe) …

Le principe d'exclusion de Pauli était, lors de sa formulation parfaitement ad hoc et les réactions initiales furent mitigées. Ultérieurement, la statistique de Fermi-Dirac (1926) l'expliqua naturellement: les électrons sont des fermions, leurs états sont antisymétriques par échange de deux électrons et ils sont donc identiquement nuls si deux électrons ont les mêmes nombres quantiques. C'est d'ailleurs Pauli lui-même qui parvint à étendre correctement la mécanique quantique de Heisenberg et Schrödinger aux particules avec spin, comme l'électron, en introduisant en 1927 les matrices "de Pauli" (W. Pauli, Zur Quantenmechanik des magnetischen Elektrons, Z. Physik 43, 601–623, 1927).

La mécanique des matrices

Knabenphysik

En 1925, Heisenberg avait 24 ans, von Neumann 22 ans, Dirac 23 ans, Jordan 23 ans, Fermi 24 ans, Pauli 25 ans, de Broglie 33 ans, mais Born 43 ans, Schrödinger 38 ans, Einstein 46 ans, Bohr 40 ans

Kramers

Le modèle de Bohr-Sommerfeld ne disait rien des transitions entre les états atomiques, à part leur énergie. Rien ne permettait de calculer l'intensité des raies par exemple (liée à la probabilité par unité de temps des transitions, es coefficients A et B d'Einstein). Une approche, initiée par Bohr lui-même (via un vague "principe de correspondance" qu'il retouchera par la suite à de multiples reprises) fut de partir de la "limite classique". Plus précisément, la fréquence du photon émis par un atome d'hydrogène lors d'une transition d'un état n à un état m est ν = ν₀ [1/n² - 1/m²], qui dépend de l'état initial mais aussi de l'état final. Mais dans la limite où n➛∞, m➛∞ mais n-m=1, ν➛ν₀/n² et ne dépend que de l'état initial n, de rayon r = r₀n² ≫ r₀. On peut alors calculer, classiquement, l'intensité de l'émission de rayonnement par un électron suivant une trajectoire circulaire de grand rayon.

Uhlenbeck, Kramers et Goudsmit

Uhlenbeck, Kramers et Goudsmit en 1928 à Ann Arbor
©AIP Emilio Segre Visual Archives.

Hendrik Kramers (1894-1952) avait rejoint en 1916 Bohr à Copenhague pour préparer sous sa direction une thèse soutenue en 1919. Sa thèse porta sur l'intensité des transitions atomiques, Kramers ayant l'idée de la relier aux coefficients de Fourier des orbites. Pour les grandes orbites quasi-classiques (n→∞), le lien intensités ⇔ composantes de Fourier est ce que la théorie classique de l'interaction matière-rayonnement prévoyait et le résultat était approximativement correct du point de vue expérimental. L'idée de Kramers était d'étendre le résultat semi-classique dans le domaine quantique, et il y travailla plusieurs années avec Bohr et les visiteurs de son Institut à Copenhague, dont Heisenberg (Kramers & Heisenberg 1925) qui utilisa cette idée comme point de départ de ses réflexions.

Kramers collabora avec Bohr jusqu'en 1926, devint alors professeur à Utrecht puis à Leyde en 1934. Il développa de nombreuses méthodes en mécanique quantique : en 1926, l'approximation de Wentzer, Kramers et Brillouin (WKB) permit de calculer des solutions de l'équation de Schrödinger, les relations de dispersion de Kramers-Krönig (1926 et 1927) jouèrent plus tard un rôle important dans le développement de la renormalisation en théorie quantique des champs.

Heisenberg

Heisenberg 1933

Werner Heisenberg (1901-1976)

Né en 1901, Heisenberg fit ses études de physique à l'université de Munich, ou enseignaient Arnold Sommerfeld et Wilhelm Wien. Il soutint sa thèse de doctorat, sur la turbulence, sous la direction de Sommerfeld en 1923. Mais avant même sa soutenance, il était venu travailler avec Max Born à Göttingen à partir de 1922 (restant nominalement l'élève de Sommerfeld qui était parti pour plusieurs mois faire une tournée de conférences aux États-Unis). Il soutint son habilitation en 1924 sous la direction de Born, via un travail sur l'effet Zeeman anormal.

Il reçut une bourse Rockefeller, lui permettant d'aller passer l'année universitaire 1924-1925 à Copenhague. Assistant (Privatdozent) à l'université de Göttingen de 1924 à 1927, il devint professeur à l'université de Leipzig en 1927, poste qu'il conserva jusquen 1945 (en y ajoutant un poste de professeur à Berlin en 1941 ?). Durant ce temps, il parvint à attirer à Leipzig un très grand nombre de doctorants et de collaborateurs (certains étant aupravant passés par Göttingen) sur des sujets très variés, des rayons cosmiques à la théorie quantique des champs et à la physique nucléaire.

Objets d'attaques de la part des nazis et des tenants de la Deutsche Physik comme Lenard ou Stark (qui voulaient purger la physique des ses "éléments juifs" comme la théorie de la relativité et la théorie quantique), il parvint à garder son poste et ses prérogatives. Il fut ensuite un élément central du programme allemand de réacteur et de bombe nucléaires.

En résidence surveillée jusqu'en 1946, il prit ensuite la direction du prestigieux Kaiser Wilhem Institut für Physik (KWI-P) replié à Göttingen. Le KWI-P fut rebaptisé Max Planck Institut en 1947 et s'installa à Munich en 1958. Heisenberg en resta directeur jusqu'en 1970, sans compter de nombreuses responsabilité dans l'administration de la recherche en Allemagne.

L'invention de la mécanique quantique

Ayant passé l'année 1924-1925 à Copenhague, avec Bohr et Kramers, pour essayer de calculer l'intensité des raies spectrales, Heisenberg n'était pas très satisfait du résultat. Il pensa que les composantes de Fourier de la décomposition des mouvements orbitaux des électrons étaient plus fondamentales que les mouvements eux-mêmes, dans la mesure où les quantités observables (énergie et intensité des raies spectrales) pouvaient apparemment être calculées à partir des seules composantes. Il voulut alors reformuler le modèle de Bohr-Sommerfeld en ne faisant intervenir que les seules composantes de Fourier, et non directement la position ou l'impulsion des électrons.

Heligoland

Victime d'une violente attaque de rhume des foins (rhinite allergique) fin mai, Heisenberg se réfugia dans l'île d'Heligoland en mer du Nord. Il raconta ensuite que les pièces du puzzle se mirent en place au cours d'une nuit d'insomnie (7 juin 1925 ?) , puis qu'il rédigea un article relativement bref d'une quinzaine de pages. À son retour début juillet à Göttingen, il en envoya une copie à Pauli et en présenta une autre à Born pour avoir son avis. Malgré sa brièveté, l'article est d'une lecture difficile en partie parce qu'il est très touffu (et parfois confus), en partie parce que Heisenberg n'avait pas alors une idée très claire de ce qu'il faisait, et en partie parce que son raisonnement passe parfois par des raccourcis plus ou moins intuitifs mais qu'il ne motivait pas.

Article de Heisenberg en 1925

Le début de l'article de Heisenberg créant la mécanique quantique

Heisenberg s'était convaincu de n'utiliser dans le calcul que des quantités directement observables, ce qui n'était pas le cas de la position de l'électron sur son orbite ou de son énergie (seules le sont les variations d'énergie d'une orbite à une autre). Étaient par contre observables les fréquences des raies et leurs intensités relatives.

Dans le modèle de Bohr-Sommerfeld, chaque raie correspond à une transition d'un électron d'un état m ➛ état n, où chaque état est repéré par un (modèle de Bohr) ou plusieurs (Bohr-Sommerfeld) nombres quantiques, qui sont des nombres entiers. On peut noter l'ensemble de ces nombres quantiques par un indice unique n sans perte de généralité. Chaque fréquence ou intensité d'une raie dépend donc de l'état initial n et de l'état final m, et peut donc s'écrire sous la forme d'un objet à deux indices: F_mn ou I_mn. Plus généralement, toutes les quantités observables sont des objets A_mn, B_mn, etc. indexés par l'état de départ et l'état d'arrivée. Toutes ces quantités A, B, etc. peuvent être rangées dans un tableau carré de la forme:

A	État 1	État 2	État n
État1	A₁₁	A₁₂	A_1n
État 2	A₂₁	A₂₁
…
État m	A_m1	A_m2	A_mn
…

Avant de se lancer dans le calcul de l'atome d'hydrogène, Heisenberg examina des modèles plus simples comme l'oscillateur harmonique (puis anharmonique) à une dimension spatiale ou le rotateur rigide à une dimension. Ce sont les modèles dynamiques les plus simples que l'on puisse étudier en mécanique.

La quantification de l'oscillateur harmonique conduit ainsi à une série de niveaux d'énergie E_n=nħ régulièrement espacés, et les quantités observables A et B sont (les composantes de Fourier de) la position X (t) et l'impulsion P(t): A_mn= X_mn et B_mn= P_mn = iM*X_mn[E_m–E_n]/ħ (l'apparition du nombre complexe i=√-1 est inévitable, de même que la constante de Planck ħ=h/2π venant de la quantification, et M est la masse de l'oscillateur, ou du rotateur).

[Attention: quand un mouvement est périodique, une analyse en composantes de Fourier (➛les harmoniques) est la procédure classique pour étudier ce genre de systèmes ☛ X(t) = ∑_j X_m exp{i ω_m t} ☛ pour un système quantifié se trouvant dans l'état n, par exemple la n° orbite de Bohr pour l'atome d'hydrogène, cela devient X_n(t) = ∑_j X_nm exp{i ω_nm t} et les deux indices n et m se réfèrent à un état. Mais on passe ensuite aux transitions entre deux états où la paire d'indices désigne les états de départ et d'arrivée. Ce glissement est à peu près justifié (Born parle de "bricolage inspiré" de la part de Heisenberg) parce que les ω_nm se révèlent être de la forme (E_n-E_m)/ħ ]

Une transition d'un état à un autre peut se faire en deux étapes (m➛j➛n), ou trois, ou plus. Il est donc indispensable d'établir des règles cohérentes pour calculer une quantité C_mn à partir des A_mj et A_jn en sommant sur tous les états j intermédiaires, et Heisenberg aboutit à quelque chose de la forme:

C_mn= ∑_j A_mj * A_jn

Mais il se heurta à une difficulté quand il eut besoin de multiplier non seulement des A entre eux, ou des B entre eux, mais des A et B entre eux. En effet la quantité C=AB obtenue différait de la quantité D=BA, ou plus explicitement:

C_mn= ∑_j A_mj * B_jn ≠ D_mn= ∑_j B_mj * A_jn

Dans son article, Heisenberg relevait cette "difficulté significative" qui n'était pas présente dans le cas classique: en particulier, le résultat du produit (des coefficients de Fourier) de la position et l'impulsion dépendait de l'ordre de la multiplication, et la différence était proportionnelle à la constante de Planck h. En effet, avec A_mn=X_mnet B_mn=iX_mn[E_m–E_n]/ħ il obtenait (pour le terme diagonal m=n après redéfinition de l'indice muet j):

∑_j { X_mj P_jm – P_mj X_jm} = M ∑_j { X_mj X_jm[E_j–E_m] – X_mj [E_m–E_j] X_jm } = ih

Vérifier!

☛ Heisenberg confia le 9 juillet 1925 son manuscrit à Max Born, pour qu'il juge de sa valeur. Celui-ci le fit parvenir le 25 juillet au Zeitschrift für Physik. Son titre un peu cryptique "Réinterprétation quantique des relations cinématiques et mécaniques" (Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen, ZP 33-879, 1925) disait exactement ce que Heisenberg pensait avoir fait: utiliser les relations cinématiques et mécaniques entre les variables de position et d'impulsion de la mécanique classique, mais en donnant un sens différent, "quantique", à ces variables devenues des objets indicés, et donc en réinterprétant leurs relations. La position d'un électron sur une orbite de Bohr (ou de la particule massive dans le cas de l'oscillateur harmonique) avait été remplacée par un objet à deux indices, indices qui se référaient aux états quantiques (orbites pour l'atome, modes harmoniques pour l'oscillateur). Heisenberg partit à Cambridge (où il exposa sa nouvelle théorie, qui stimula l'intérêt de Dirac) puis il retourna à Copenhague passer l'été.

☛ Pendant son absence, Max Born reformula les calculs de Heisenberg après avoir identifié dans les variables indicées imaginées par Heisenberg des matrices, et les étranges règles de multiplication des variables étaient les règles normales de multiplication des matrices. Born ne fut pas non plus surpris de la non-commutativité de la multiplication, courante pour des matrices. Les mathématiciens utilisaient depuis plus d'un siècle les matrices (leur nom fut donné en 1850 par Sylvester) en particulier pour résoudre des systèmes d'équations à plusieurs inconnues, mais leur usage était alors pratiquement inconnu en physique. Minkowski les avait cependant utilisées en 1908 et Born lui-même en 1909, puis à nouveau en 1921 (en cristallographie).

En explicitant les règles du calcul matriciel et la non-commutatitivité des opérations, Born démontra en particulier que l'équation de non-commutativité écrite par Heisenberg pour les composantes de la position et de l'impulsion

∑_j { X_mj P_jm – P_mj X_jm} = ħ

était égale à zéro pour les termes non-diagonaux et que l'on pouvait l'écrire bien plus simplement:

XP – PX = iħ I

X et P étant les matrices correspondant à la position et à l'impulsion, et I étant la matrice identité (tous les termes diagonaux sont égaux à 1 et tous les termes non-diagonaux égaux à zéro, de sorte que, multipliée ou multipliant n'importe quelle matrice, elle redonne cette matrice). Cela montre clairement comment la constante de Planck fixe l'échelle des phénomènes quantiques. Born montra également comment les matrices X et P dépendent du temps, chaque élément de matrice X_mn(t) évoluant comme une onde plane:

X_mn(t) = X_mn(0) exp{i(E_m–E_n]/ħ t}

☛ Épuisé, Born partit en cure de repos et confia à son doctorant Pascual Jordan la suite de la mise en forme. Jordan (1902-1980) avait été l'assistant de Richard Courant à Göttingen pendant la préparation du traité de Courant & Hilbert Les méthodes de la physique mathématique publié en 1924, et qui contenait fortuitement la pluprt des techniques qu'allait requérir la nouvelle théorie quantique. David Hilbert, consulté au sujet des matrices, avait dit à Born et à Jordan que le seul cas où le smatrices lui avaient été utiles, c'était dans la résolution de certaines équations différentielles et qu'ils avaient sans doute affaire à un problème similaire sous-jacent. Born dit plus tard à Edward Condon que, s'il avait pris au sérieux la remarque de Hilbert, ils auraient sans doute directement abouti à la théorie de Schrödinger, avec six mois d'avance.

Au cours des années suivantes, Jordan allait se tourner vers les mathématiques (algèbres de Jordan) puis la cosmologie et la géologie plus tard. Son engagement dans le parti nazi et les SA devait le marginaliser durablement (ironiquement, les nazis le jugeaient politiquement peu fiable du fait de sa longue collaboration avec des Juifs comme Courant, Born et Pauli). En 1945, Born lui refusa une lettre de recommandation pour qu'il retrouve son poste lors de la dénazification (lettre que Heisenberg lui écrira, ainsi que Pauli). Il fut ensuite membre du parti conservateur CDU, élu député au Bundestag et défenseur d'une remilitarisation nucléaire de l'Allemagne en 1957.

Jordan poursuivit donc pendant l'été 1925 la mise en forme des idées de Heisenberg revues par Born, et il envoya en septembre le résultat à la même revue Zeitschrift für Physik (M. Born et P. Jordan, Zur Quantenmechanik, ZP 34-858, 1925). Cet article commence par un hommage au travail de Heisenberg, puis expose les règles du calcul matriciel et l'équation d'évolution temporelle des matrices. La part respective de Heisenberg, de Born et de Jordan est difficile à démêler, et ceci est rendu plus difficile par l'évolution ultérieure des carrières des trois physiciens lors de l'arrivée au pouvoir de Hitler en 1933: Born émigra en Grande-Bretagne et acquit la nationalité britannique, Heisenberg resta en Allemagne en gardant une certaine neutralité en apparence, et Jordan rejoignit le parti nazi. Heisenberg reçut le prix Nobel de physique de 1932 (décerné en 1933) "pour la création de la mécanique quantique".

☛ Heisenberg, Born et Jordan rédigèrent une synthèse détaillée de la "mécanique des matrices" reçue le 16 novembre (Zur Quantenmechanik II, Zeitschrift für Physik 35-557, 1925). Surnommée le Dreimannerarbeit, elle contient explicitement l'équation donnant l'évolution temporelle d'une quantité A (représentée par une matrice):

∂A/∂t = –i/ħ [A,H] où H est l'opérateur hamiltonien du système (également sous forme matricielle)

☛ Application immédiate à l'atome d'hydrogène par Wolfgang Pauli (W. Pauli, Über das Wasserstoffspectrum vom Standpunkt der neuen Quantenmechanik Zeitschr. Phys., 36, 336, 1926) et indépendamment par Paul Dirac (Quantum mechanics and a preliminary investigation of the hydrogen atom, Proc. R. Soc. London, Ser. A 110-561 1926)

☛ Dès la fin de 1925, Born s'était lancé dans l'extension de la mécanique des matrices (inventée pour des processus oscillatoires) à des processus non stationnaires comme les collisions entre particules. En collaborant avec Norbert Wiener au cours d'un séjour au M.I.T., il généralisa les matrices en opérateurs linéaires (Dirac fit la même chose en parallèle). Puis il trouva ensuite que l'approche de Schrödinger, la mécanique ondulatoire, était d'un emploi plus souple que les matrices, et il aboutit ainsi à son interprétation de la fonction d'onde comme densité de probabilité.

Mécanique des matrices

Toutes les quantités observables sont des objets indexés par l'état de départ et l'état d'arrivée. Donc des matrices n*n à coefficients a priori complexes.

Valeurs propres = valeurs possibles que peuvent avoir les observables (valeurs réelles ⇔ matrices hermitiennes = égales à leur transconjuguée)
Vecteurs propres = états possibles du système correspondant aux valeurs propres
Mesure = observation d'une valeur et une seule ⇔ réduction de l'état du système après mesure au vecteur propre correspondant

Mesure simultanée de deux observables ⇒ vecteur propre commun aux deux observables. En général, il n'en existe pas ⇒ impossibilité de mesurer simultanée de deux observables ⇒ inégalités de Heisenberg

Paul Dirac

Dirac

Paul Adrien Maurice Dirac (1902-1984)

Le père de Paul Dirac était originaire du canton du Valais , en Suisse romande, et il s'était établi à Bristol en Grande-Bretagne comme professeur de français dans un lycée technique. Paul fut un élève très brillant, passionné par les mathématiques, la physique et la chimie, et il reçut une formation d'ingénieur en électrotechnique à l'université de Bristol. Diplômé, mais sans travail, il obtint une petite bourse lui permettant de suivre une maîtrise de mathématiques à Bristol de 1921 à 1923, avant d'obtenir une bourse plus importante lui permettant d'entrer à l'université de Cambridge pour y faire un doctorat sous la direction du théoricien Ralph Fowler (1889-1944), le gendre d'Ernest Rutherford. Fowler était un spécialiste de thermodynamique et de physique quantique, surtout dans le domaine de l'astrophysique, collaborant avec Milne, Eddington, Chandrasekhar et McCrea.

Fowler avait assisté au séminaire donné en juillet 1925 à Cambridge par Heisenberg sur sa nouvelle théorie, et il avait transmis une copie de l'article de Heisenberg à Dirac, alors en vacances chez ses parents à Bristol. L'intérêt de Dirac fut stimulé par le commutateur [X,P]=XP-PX, qui apparaissait sous une forme quelque peu obscure dans le texte de Heisenberg, car cela lui évoqua les crochets de Poisson de la mécanique classique dans sa formulation hamiltonienne. Dans ce cas en effet, un système est défini par son espace de phase (positions q et moments conjugués p) et le crochet de Poisson {A,B} de deux variables A(p,q) et B(p,q) est défini par:

{A,B} = ∂A/∂q ∂B/∂p – ∂A/∂p ∂B/∂q

D'où {q,q} = 0 , {p,p} = 0 mais {q,p} = 1 .

et la variation au cours du temps d'une quantité f(p,q,t) est donnée par

df/dt = {f,H} + ∂f/∂t

où H(p,q,t) est la fonction de Hamilton du système considéré.

Dirac fit alors l'hypothèse que l'on pouvait passer de la physique classique à la physique quantique simplement en remplaçant les crochets de Poisson par des commutateurs de matrices (au iħ près), puis que ces matrices n'étaient qu'un cas particulier (quand les états étaient discrets) d'objets plus généraux, des opérateurs linéaires agissant sur des éléments d'un espace vectoriel, éléments que l'on pouvait identifier aux états quantiques. Cette réanalyse de l'article de Heisenberg conduisait à une simplification considérable du formalisme et facilitait sa généralisation. À ce moment là (août et septembre 1925), Dirac n'avait pas connaissance des analyses de Born et de Jordan, mais il avait redécouvert indépendamment leurs résultats, sous une forme plus simple.

Les crochets de Poisson {A,B} donnent une structure d'algèbre à l'ensemble des fonctions A, B… (on peut additionner des crochets de Poisson: {A,B} + {A,C} = {A,B+C} et on peut les multiplier par un nombre réel: a{A,B} = {aA,B} = {A,aB}). Les commutateurs de Dirac donnent également une structure d'algèbre à l'ensemble des opérateurs équivalents A, B… mais une algèbre complexe maintenant à cause de l'apparition du facteur i .

[A,B] = AB – BA ➛ [P,P] = 0 , [Q,Q] = 0 mais [P,Q] = -iħ I

Comme ħ est une quantité très petite, la non-commutatitivité de la position Q et du moment conjugué P (l'impulsion dans les cas simples) n'avait pas été remarquée plus tôt.

Fowler conseilla à Dirac de publier très vite son étude, ce qu'il fit aussitôt (P.A.M. Dirac, The fundamental equations of quantum mechanics, Proc. Roy. Soc. A, 109-642, 1925), tout en envoyant une copie à Heisenberg qui en fut enthousiaste. Bizarrement, Heisenberg ne mentionna pas à Dirac ce que Born et Jordan avait accompli entretemps et lorsque Dirac reçut le prix Nobel de physique en 1933 (en principe pour ce travail, bien qu'il eût entretemps publié bien d'autres résultats essentiels), Born en fut anéanti car il estimait bénéficier de l'antériorité, et au moins que son travail soit reconnu égal. Il avait également été profondément déçu que le prix Nobel de physique aille en 1932 au seul Heisenberg, jugeant son apport essentiel (Heisenberg partageait d'ailleurs ce jugement).

Dirac dériva ensuite le spectre de l'atome d'hydrogène (Quantum mechanics and a preliminary investigation of the hydrogen atom, Proc. Roy. Soc. A, 110-561, 1926), parallèlement à Pauli. Puis il s'attaqua aux atomes à plusieurs électrons, ainsi qu'à l'effet Compton (indiquant que les observations de Compton devaient être légèrement inexactes, ce que Compton confirma immédiatement par de nouvelles mesures).

Ce travail fit l'objet de sa thèse de doctorat en 1926. En 1927, il publia la première dérivation des coefficients A et B d'émission spontanée et stimulée introduits par Einstein (The quantum theory of the emission and absorption of radiation, Proc. Roy. Soc. A114-243), et il introduisit à cette occasion les opérateurs de création et d'annihilation, qui forment la base d ela théorie quantique des champs..

En 1928 il écrivit une équation relativiste pour l'électron, l'équation de Dirac (The quantum theory of the electron, Proc. Roy. Soc. A117-610). Cette équation lui permit de comprendre l'origine du spin, et de prévoir l'existence des antiparticules (confirmée par la découverte du positron en 1932). Il fut ainsi le fondateur de l'électrodynamique quantique.

Son traité Les principes de la mécanique quantique en 1930 exposait de la façon la plus claire les mécanismes de base de la théorie, et le vocabulaire et les notations de Dirac sont devenues omniprésents. Cet ouvrage a été réédité, et amélioré à plusieurs reprises (la dernière fois en 1967). Il fut aussi l'inventeur de la fonction δ de Dirac (qui n'est pas une fonction mais une distribution) nulle partout sauf à l'origine où elle est infinie. Professeur à Cambridge sur la chaire "lucasienne" de mathématiques appliquées (celle de Newton) de 1932 à 1969, Dirac y apporta d'importantes contriutions à la théorie quantique des champs, en particulier quant à la question de la quantification d'un système soumis à des contraintes (de symétrie par exemple). Mais il n'accepta jamis la validité des méthodes de renormalisation pour se débarrasser des infinis ("on ne fait que les cacher sous le tapis" disait-il). En 1970, il rejoignit l'université de Floride à Tallahassee. Dirac épousa la soeur d'Eugene Wigner, Manci, en 1937.

Dirac était célèbre pour son extrême timidité (partagée avec Wigner), sa très grande modestie, et son côté taciturne. Les anecdotes à ce sujet sont nombreuses: il n'appela jamais la statistique de Fermi-Dirac autrement que "la statistique de Fermi", il s'étonna de l'intérêt d'Oppenheimer pour la poésie en expliquant que la science avait pour but de rendre clair un sujet confus alors que la poésie avait le but opposé. On dit que lors d'une conférence qu'il donnait, un participant intervint "Professeur Dirac, je n'ai pas compris comment vous avez dérivé cette équation" et que, comme Dirac restait silencieux, le président de séance lui demanda "Vous ne voulez pas répondre à la question?". La réponse de Dirac fut "Ce n'était pas une question, c'était une déclaration." Lors d'une discussion en marge de la conférence Solvay de 1927, Einstein, Planck, Pauli, Heisenberg et Dirac abordèrent la question de la religion et de la foi. Selon Heisenberg, l'intervention de Dirac les étonna par sa violence: Dirac jugeait ces croyances futiles, reliquats d'une époque de ténèbres intellectuelles, mais malheureusement très utiles spour maintenir les peuples dans leur docilité. Pauli brisa le silence embarrassé en déclarant: "Eh bien, notre ami Dirac a une religion, dont l'acte de foi est: Il n'y a pas de Dieu, et Dirac est son prophète!"

Inégalités de Heisenberg (1927)

Mesure ⇒ vecteur propre de l'observable. Observables (matrices) ne commutant pas = cas général.

Ordre des observations ⇒ résultats différents (différence proportionnelle au commutateur des matrices)

⇒ inégalités de Heisenberg

Inégalités de Heisenberg

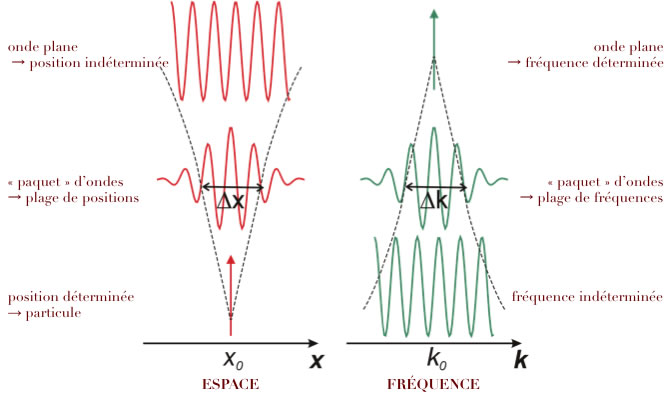
Mécanique ondulatoire (Wellenmechanik)

En partant des travaux de Kirchhoff en 1859, la physique de l'interaction entre matière et rayonnement suivit deux branches qui ne se réunifièrent que tardivement:

l'étude de l'émission continue, thermique, qui conduisit Stefan (1879), Boltzmann (1884), et Wien (1894) à établir les lois du "corps noir", puis Planck (1900) et surtout Einstein (1905) au "quantum de lumière". Cette branche mena ensuite de Broglie (1923) et Schrödinger (1926) à la mécanique ondulatoire.
l'étude des raies spectrales, où les travaux de Kirchhoff et Bunsen (1860), Balmer (1885), Rydberg (1888) conduisit Bohr à proposer en 1913 son modèle atomique, puis Heisenberg, Born et Jordan la mécanique des matrices en 1925.

Schrödinger montra dès 1926 l'équivalence entre son approche et celle de Heisenberg, puis Dirac ouvrit la voie à l'électrodynamique quantique en 1927.

Louis de Broglie (1892-1987)

Louis de Broglie

Maurice, duc de Broglie (1875-1960) fut un physicien expérimentateur de premier plan et un spécialiste de la diffraction des rayons X et de l'ionisation des gaz. Élève de Paul Langevin, il fut secrétaire du premier Congrès Solvay en 1911, académicien et professeur de physique générale au Collège de France, prenant la succession de Langevin. Après la Première guerre mondiale, il installa chez lui un laboratoire de physique où il forma son frère cadet, Louis.

Louis, prince puis duc de Broglie (l'aîné de la famille porte le titre de duc, le cadet celui de prince) avait suivi des études d'histoire avant de se tourner vers les mathématiques et la physique. Il avait beaucoup étudié les ressemblances entre les lois de l'optique ondulatoire et le principe de Fermat d'une part, et le principe de Maupertuis d'autre part conduisant à la formulation es lois de la mécanique donnée par Hamilton en 1827. Il pensa que cette similitude n'était pas une pure coïncidence et qu'elle devait refléter une analogie profonde.

De Broglie partit des réflexions d'Einstein sur les quanta de lumière. La lumière se comportait manifestement comme une onde dans certaines circonstances (phénomènes de diffraction et d'interférence), et manifestement comme une particule dans d'autres circonstances (effet photoélectrique, diffusion Compton). Ce deuxième aspect avait été difficile à détecter, et à admettre, et de Broglie se demanda si une erreur inverse n'avait pas été commise pour l'électron: le considérer uniquement comme une particule et négliger son aspect ondulatoire.

☞ Si l'électron pouvait se comporter comme une onde dans certaines circonstances, à l'intérieur d'un atome par exemple, cela permettrait peut-être d'expliquer son comportement surprenant pour une particule matérielle. Dans le cas de la lumière, la fréquence avait été la propriété d'où l'impulsion et l'énergie avaient été déduites (ν ➛ p=hν/c=h/λ et E=hν). Dans le cas de la matière, les propriétés de départ sont la masse M et la vitesse V d'où sont déduites l'impulsion p = MV et l'énergie E = MV²/2 . Mais quelle fréquence ou quelle longueur d'onde λ associer à une telle particule matérielle? De Broglie calqua audacieusement en 1923 la relation λ = h/p vraie pour un photon en associant à un électron de vitesse V une onde dont la longueur d'onde serait:

λ = h/p = h/MV (longueur d'onde de de Broglie)

Le terme "associer" est intentionnellement vague: à ce stade, il n'est pas possible de dire que l'électron est une onde, mais seulement qu'une onde lui est associée sans que sa nature soit précisée, ni les conditions de la correspondance particule ⇌ onde. L'objectif de de Broglie fut de construire une mécanique ondulatoire qui généraliserait la mécanique des particules de la même façon que l'optique ondulatoire généralise l'optique géométrique. La présence de la constante de Planck h dans la relation λ = h/p expliquait pourquoi les effets ondulatoires de la matière n'étaient pas perceptibles macroscopiquement: "à titre d’exemple, calculons la longueur d’onde de de Broglie assocíée à un moustique en vol. La masse d’un moustique est de l’ordre du milligramme, et on peut estimer sa vitesse à 0.1 m/s. On trouve alors une longueur d’onde de l’ordre de 10⁻²⁷ m." (F. Besnard, cours EPF 2012)

Ceci permit à Louis de Broglie d'expliquer immédiatement la règle de quantification de Bohr MV_nR_n=nħ=nh/2π. En effet, elle se réécrit

2π r_n = nh/MV_n = nλ

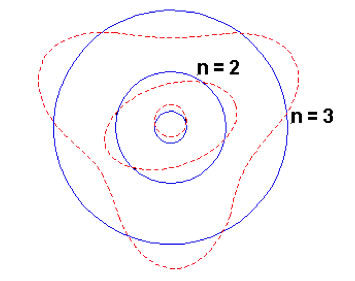
Ondes de de Broglie

Ceci signifiait que les seules orbites stationnaires dans un atome sont celles qui correspondent à un nombre entier de longueurs d'ondes, exactement comme les états stationnaires des modes de vibration en mécanique classique. L'idée d'onde associée à l'électron permettait ainsi d'expliquer, en partie, les bizarreries du modèle de Bohr-Sommerfeld. Par ailleurs, elle rétablissait une symétrie entre matière et rayonnement. Le caractère radical de l'hypothèse de de Broglie perturba d'ailleurs quelque peu son jury de thèse, en particulier Jean Perrin et Paul Langevin. Ce dernier demanda l'avis d'Einstein, qui fut imméditement emballé, déclarant "Il a levé un pan du grand voile!". De Broglie obtint sa thèse le 29 novembre 1924. Mais Bohr ne fut pas du tout convaincu (ses relations avec de Broglie étaient demeurées médiocres en raison d'un différent scientifique antérieur), et par contrecoup la majorité des physiciens du domaine resta réticente, jusqu'à ce que Schrödinger change la donne. Louis de broglie reçut le prix Nobel de physique dès 1929 (avant Heisenberg en 1932 et Schrödinger en 1933).

Le raisonnement de de Broglie fut en fait un peu plus subtil que de poser simplement λ = h/p. Il partit d'un corpuscule libre immobile, en lui attribuant une fréquence ν₀ = E₀/h = Mc²/h correspondant à son énergie de masse . En changeant de référentiel (transformation de Lorentz) pour celui où le corpuscule a une vitesse V, son énergie devient E = E₀/√(1-V²/c²) et la fréquence associée ν = ν₀/√(1-V²/c²). Mais le corpuscule a aussi une impulsion

p = MV/√(1-V²/c²) = hν/V = h/λ [Attention à la subtilité vitesse de phase V ≠ vitesse de groupe v ☛ À REVOIR!]

Puis de Broglie examina le cas où il y a un champ de force dérivant d'un potentiel, effectue les mêmes transformations de Lorentz et montra que la vitesse de groupe des ondes est à nouveau égal à la vitesse du corpuscule. Il établit ainsi un parallèle entre le principe de Fermat pour l'onde et le principe de moindre action pour le corpuscule, montrant que les trajectoires du corpuscule sont identitiques aux trajectoires de rayons de l'onde associée. C'est alors seulement qu'il identifia la condition de quantification de Bohr-Sommerfeld et la condition de stationarité de l'onde associée. L'apparition de nombres entiers est alors automatique. De Broglie conclut en notant que son formalisme s'applique aussi bien à un corpuscule de masse nulle: dans ce cas la vitesse de phase et la vitesse de groupe tendent toutes les deux vers c quand la masse tend vers zéro, et il retrouva ainsi les relations d'Einstein E = hν et p = hν/c.

Ayant montré que les lois de la mécanique étaient l'équivalent des lois de l'optique géométrique,et notant que celles-ci ne sont que la limite de la "vraie" théorie ondulatoire pour des dimensions grandes devant la longueur d'onde, de Broglie en déduisit qu'il devait exister l'équivalent des phénomènes de diffraction et d'interférence pour les corpuscules quand les dimensions du système approchaient de la longueur d'onde associée (la longueur d'onde de de Broglie dans le vocabulaire moderne). Il calcula que la longueur d'onde associée à un électron d'énergie 1 eV était de 12.2*10¹⁰ m, soit les dimensions atomiques, ou d'une maille cristalline, ou des rayons X. D'où l'idée d'effectuer avec des électrons des expériences de diffraction sur des cristaux, analogues à celles de Max von Laue en 1914 avec des rayons X.

Pour de Brogie, les ondes associées à l'électron avaient une réalité physique, quasi-matérielle. Elles devaient suivre une équation d'onde déterministe, dépendant de variables "cachées", et déterminer le comportement de la particule associée, jouant le rôle d'onde-pilote. De Broglie ne donnait cependant pas cette équation pour les ondes de matière, suscitant les critiques de Peter Debye mais incitant Schrödinger à en rechercher une. L'idée d'onde-pilote fut violemment critiquée par Pauli lors du congrès Solvay de 1927, et de Broglie n'y revint que lorsque David Bohm (1917-1992) présenta en 1952 une théorie cohérente de la paire particule/onde pilote.

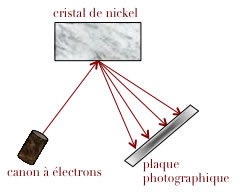
Expériences de Davisson et Germer (1927) et de George Paget Thomson

L'expérience de Clinton Davisson et Lester Germer démontra en 1927 la nature ondulatoire de l'électron en mesurant la longueur d'onde par la même méthode qui permet de mesurer la longueur d'onde de rayons X: par diffraction sur un cristal de nickel et en observant les figures de diffraction de Bragg.

Expérience de Davisson et Germer

Résultat de Davisson

Clinton Davisson (1881-1958) contribua ensuite au développement du microscope électronique qui utilise explicitement l'aspect ondulatoire de l'électron. Il partagea le prix Nobel de physique en 1937 avec George Thomson.

George Paget Thomson (1892-1975) était le fils de J.J. Thomson, découvreur de l'électron, et il commença sa carrière au laboratoire Cavendish avant de devenir professeur à Aberdeen puis à l'Imperial College de Londres. En 1928, il diffusa des électrons à travers des poudres métalliques (la méthode imaginée par Debye et Scherrer pour la diffraction des rayons X) et confirma ainsi leur nature ondulatoire. Il contribua beaucoup ensuite à l'étude des neutrons, puis il fut en 1940 le responsable du comité MAUD chargé d'explorer la possibilité d'une arme nucléaire.

Il est également possible de faire interférer des électrons:

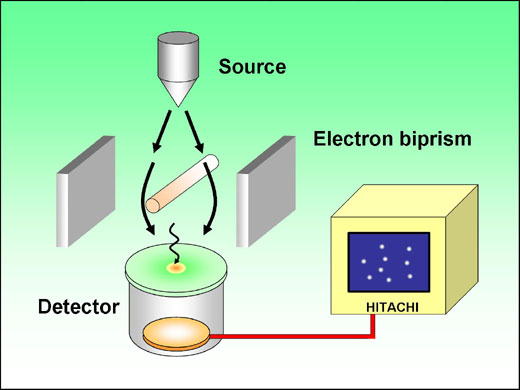
Interférence d'électrons

Dans cette expérience contemporaine (Dr. Akira Tonomura, société Hitachi) les électrons déviés par le filament central dessinent une figure d'interférence sur le déteccteur. C'est l'équivalent de l'expérience des trous d'Young ou du biprisme de Fresnel en optique classique.

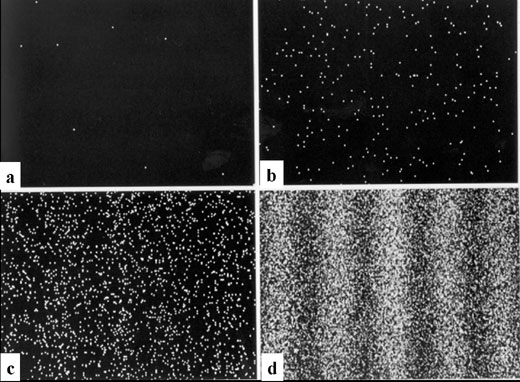
Interférence d'électrons

Les électrons arrivent un par un sur le détecteur, et la figure classique des franges d'interférence n'apparaît que peu à peu: 20 minutes séparent la figure a (8 électrons enregistrés) de la figure d (160 000 électrons).

Les multiples facettes du Professeur Schrödinger

Schrödinger

Erwin Schrödinger (1887-1961)

Premiers travaux

En 1926, Schrödinger n'était pas un débutant. Élève à Vienne de Friedrich Hasenöhrl (1874–1915) qui fut tué pendant la Première guerre mondiale, et de Franz Exner (1849–1926), il en devint l'assistant, travaillant sur des questions d'électricité atmosphérique (son sujet de thèse en 1910 était Sur la conduction de l'électricité sur la surface des isolateurs dans l'air humide), de mouvement brownien et de statistiques. Il examina la radioactivité de l'atmosphère à différentes altitudes et la relia à la distribution avec l'altitude de divers corps radioactifs. Avec Fritz Kohlrausch, Schrödinger étudia aussi l'émission des rayonnements bêta par des gammas incidents sur des métaux. Il obtint son habilitation en 1914, avant de passer la guerre comme officier d'artillerie de l'armée autro-hongroise. Il s'intéressa beaucoup à cette période à la théorie de la vision des couleurs, thème sur lequel il revint régulièrement jusqu'à la fin de sa vie.

En 1920, il fut brièvement l'assistant de Max Wien (cousin de Wilhelm Wien) à Iéna, puis professeur à Stuttgart, Breslau puis Zürich en 1921, avant de succéder en 1927 à Berlin à Max Planck. C'est à ce moment qu'il s'intéressa de près au modèle de Bohr-Sommerfeld et qu'il l'appliqua aux métaux alcalins (sodium, potassium...). En 1922, il utilisa les techniques géométriques suggérées par Hermann Weyl (lui aussi professeur à Zürich) à l'étude des orbites des électrons. Toute sa vie, Schrödinger demeura favorable à l'idée que les lois de conservation (de l'énergie en particulier) ne sont que des lois statistiques qui peuvent être violées dans de rares occasions (idée acquise d'Exner), et il fut donc un partisan du modèle de Bohr-Kramers-Slater (vite réfuté par les expériences de Geiger et Bothe). En 1924-1925, il s'intéressa aux idées d'Einstein sur la statistique des gaz, avant de découvrir les idées de Louis de Broglie.

Une vie personnelle atypique

Bien que son mariage en 1920 avec Annemarie Bertel fût relativement heureux, tous deux eurent des relations multiples (et fréquemment durables), Annemarie avec Hermann Weyl en particulier, et Erwin avec Hildegarde March, épouse de son collaborateur Arthur March(1891-1957), tous vivant à certains moments sous le même toit. Hilde l'avait d'ailleurs accompagné au sanatorium d'Arosa (Schrödinger souffrit toute sa vie de tuberculose), où il établit l'équation qui porte son nom. Schrödinger eut d'ailleurs une fille de chacune de ses deux compagnes en 1933 et en 1934 (ainsi que d'au moins deux de ses étudiantes quand il fut professeur à Dublin). Quand il quitta l'Allemagne en 1933, il partit avec toutes les deux, ainsi qu'avec Arthur March pour qui il demanda un poste d'assistant à Oxford où lui-même venait d'obtenir un poste. Malgré le prestige que lui apporta le prix Nobel de physique en 1933, les autorités universitaires d'Oxford n'apprécièrent pas sa vie personnelle atypique, ni celles de Princeton qui lui avaient offert un poste en 1934. Il retourna brièvement en Autriche, à Graz en 1936, puis repartit après l'Anschluss à Oxford, Gand puis finalement Dublin en 1940 à l'invitation d'Eamon de Valera. Il y resta jusqu'à sa retraite en 1956, puis il retourna à Vienne.

Schrödinger et sa vie privée

1926: une année exceptionnelle

Fortement impressionné par la thèse de doctorat de Louis de Broglie, Schrödinger la présenta à plusieurs reprises lors de séminaires en octobre et novembre 1925. Mais l'absence d'une équation d'onde pour les ondes de de Broglie était un gros handicap, comme Peter Debye lui fit paraît-il remarquer [Debye était à Zurich??], et il profita d'un séjour au sanatorium d'Arosa au cours de l'hiver 1925-1926 pour s'attaquer au problème.

☛ Décembre 1925: "Zur Einsteinschen Gastheorie" explique la satistique de Bose-Einstein en termes d'ondes de matière quantifiées. Les particules ne sont que des paquets d'ondes (Schrödinger s'intéresse à la possible dispersion du paquet d'ondes) et il n'y pas dualité particule-onde comme chez Einstein ou de Broglie.

☛ Janvier 1926: "Quantisierung als Eigenwertproblem". Schrödinger ne parvient pas à écrire une formulation relativiste pour les ondes, et remet la question à plus tard. Quatre articles successifs au long de l'année (Ann. Phys. 79-361, Ann. Phys. 79-489, Ann. Phys. 80-437 et Ann. Phys. 81-109):

Equation de Schrödinger indépendante du temps et application aux niveaux d'énergie de l'atome d'hydrogène
Oscillateur harmonique, rotateur rigide, et molécule diatomique
Calcul perturbatif ☛ solutions approchées, effet Stark
Équation de Schrödinger dépendant du temps. Interprétation de la fonction d'onde (ou son module au carré) comme une densité de masse ou de charge de l'électron.

☛ Mars 1926: "Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinen"(Sur le rapport entre la mécanique quantique de Heisenberg-Born-Jordan et la mienne, Ann. der Phys., 79-734) où il montre que les matrices peuvent être interprétées comme des opérateurs agissant dans l'espace des solutions de son équation. Il y spécule également sur la possibilité d'une compréhension classique de l'intensité du rayonnement émis par les atomes une fois mieux comprise la relation entre matière et rayonnement.

☛ Mars? 1926: "Der stetige Übergang von der Mikro- zur Makromechanik" (La transition continue de la micro à la macro-mécanique) Die Naturwissenschaften, 14. Jahrg. Heft 28, S. 664-1926). Construction d'une particule comme un "paquet d'ondes", une superposition cohérente d'ondes, dont Schrödinger montra la stabilité au cours du temps, dans certaines conditions, et il l'applica à la diffusion de particules

Un chat célèbre

Son interprétation très matérielle des ondes de matière, selon laquelle les particules ne sont que des paquets d'ondes localisés, fut vite rejetée au profit de l'interprétation statistique avancée par Max Born, mais Schrödinger ne s'y rallia jamais. Certes, la fonction d'onde ψ ne "vit" pas dans l'espace physique mais dans l'espace de phase, mais cela ne semblait pas essentiel à Schrödinger. En 1935, dans un article faisant le point sur la théorie quantique et ses interprétations, il suggéra la célèbre expérience (de pensée!) du "chat mort et vivant" destinée à démontrer l'absurdité de l'interprétation probabiliste de la fonction d'onde et des idées défendues par Bohr et Heisenberg.

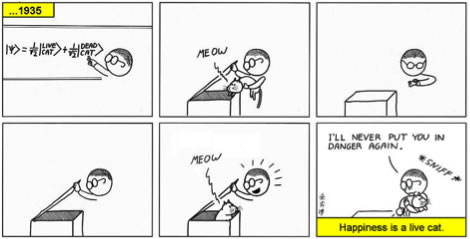
L'expérience du chat de Schrödinger

L'expérience du chat de Schrödinger, vue par Abstruse Goose

Des centaines (milliers ?) de livres, articles et plaisanteries diverses s'ensuivirent...

Qu'est-ce que la vie ?

À Dublin, Schrödinger travailla sur une théorie unifiée de la gravtiation et de l'électromagnétisme, entretenant une correspondance suivie avec Einstein sur la question, et il crut y être arrivé en 1947, avant qu'Einstein lui montre son erreur.

Schrödinger fut aussi toute sa vie passionné de philosophie, celle de Schopenhauer d'abord, puis Spinoza et Kant avant de se tourner vers la fin de sa vie vers la philosophie hindoue, les Upanishads en particulier. Il exprima à plusieurs reprises (entre autres dans son livre de 1961 Ma conception du monde) sa conviction que la métaphysique était essentielle au physicien pour construire une image cohérente du monde.

Schrödinger était cependant athée, et il présenta en 1944 dans Qu'est-ce que la vie? une approche résolument matérialiste de la vie. Par un raisonnement de pur physicien et partant des idées de Max Delbrück sur la génétique des virus et des bactéries (qu'il contribue à populariser), il conclut à l'existence dans les chromosomes d'un "cristal apériodique", une macromolécule stable qui, au coeur des cellules, puisse se répliquer à l'identique et se transmettre immuable de génération en génération. Ce livre incita de nombreux physiciens (dont Max Delbrück et George Gamow sont les plus célèbres) à s'intéresser de près à la génétique moléculaire, et il influa beaucoup sur Crick, Watson et Wilkins. Il anticipait la découverte de la structure en double hélice de l'ADN une décennie plus tard puis du "code génétique". Schrödinger poursuivit en 1956 dans L'esprit et la matière sur le rôle de la conscience et de l'éthique sur le développement darwinien, l'unité de la conscience, et la place de la religion.

Équation de Schrödinger

En décembre 1925, Schrödinger commença par rechercher une équation d'onde relativiste pour l'électron, en partie calquée sur celle de l'électromagnétisme (dérivées secondes par rapport à l'espace et au temps). Redérivée de nombreuses fois plus tard, en particulier par Oskar Benjamin Klein (1894–1977) et Walter Gordon (1893–c.1940), elle est connue sous le nom d'équation de Klein-Gordon. Pauli et Weisskopf montrèrent en 1934 qu'elle décrit en fait des particules de spin zéro.

Mais elle ne donnait pas les bons résultats pour l'atome d'hydrogène, et Schrödinger finit par aboutir à une équation qui donnait le bon résultat, mais elle était non-relativiste (dérivée première par rapport au temps mais dérivées secondes par rapport à l'espace). Il apparut ensuite que l'origine des difficultés de Schrödinger se trouvait dans le spin de l'électron, dont il n'avait pas tenu compte: le couplage spin-orbite compense, en partie, les corrections relativistes, et son équation non-relativiste sans spin donne pour l'atome d'hydrogène presque le même résultat que l'équation relativiste avec spin de Dirac!

Schrödinger repartit non de l'équation d'onde pour la lumière, mais des équations de Maxwell que l'on peut écrire:

∂E/∂t = ∇xB et ∂B/∂t = -∇xE

où l'opérateur nabla ∇ a pour composantes (∂/∂x, ∂/∂y, ∂/∂z) en coordonnées cartésiennes. Schrödinger chercha donc une équation de la forme

∂ψ/∂t = F(ψ)

où F ferait intervenir la fonction d'onde ψ et ses dérivées par rapport à l'espace. Mais F doit être telle que l'équation ait parmi ses solutions des ondes planes, qui s'écrivent:

ψ(x,t) = ψ(0) exp i {k.x - ωt}

avec un nombre d'onde k relié à l'impulsion p par k = p/ħ et une pulsation ω reliée à l'énergie par ω = E/ħ [relation pulsation-fréquence ω= 2πν]. Comme E=p²/2m, la relation de de Broglie s'écrit ω = ħk²/2m.

➡ ∂ψ/∂t = - iω ψ = -i (ħk²/2m) ψ = F(ψ)

Comme ∂ψ/∂x = ik ψ cela suggère que F contienne une dérivée seconde par rapport à l'espace

➡ ∂²ψ/∂x² = -k² ψ

➡ F(ψ) = i ħ/2m ∂²ψ/∂x² pourrait donc faire l'affaire. Et en 3 dimensions ∂²/∂x² ➛∂²/∂x²+∂²/∂y²+∂²/∂z² ≣ ∇² = ∆ (opérateur de Laplace, ou laplacien).

➡ ∂ψ/∂t = i ħ/2m ∆ψ ⇔ i ħ ∂ψ/∂t = – ħ²/2m ∆ψ

Ceci est l'équation de Schrödinger pour une particule libre (sans interaction).

Schrödinger

Particule interagissant avec un potentiel

Schrödinger remarqua la correspondance entre impulsion p et opérateur différentiel ∂/∂x, ou plus précisément p ⇔ –i ħ ∂/∂x, permettant à l'équation pour la particule libre de s'écrire

i ħ ∂ψ/∂t = [p²/2m] ψ = E_cinétique ψ

suggérant la généralisation

i ħ ∂ψ/∂t = [E_cinétique + E_potentielle] ψ = H ψ

où H est le hamiltonien. D'où l'équation de Schrödinger complète:

➡ i ħ ∂ψ/∂t = H ψ

Quand les forces agissant sur la particule dérivent d'un potentiel V, E_potentielle = V(x) et

➡ i ħ ∂ψ/∂t = [p²/2m + V(x)] ψ

➡ i ħ ∂ψ(x,t)/∂t = – ħ²/2m [∂²/∂x²+∂²/∂y²+∂²/∂z²] ψ(x,t) + V(x)ψ(x,t)

Schrödinger n'a pas réellement démontré que cette équation était la bonne, mais elle conduit à d'excellents résultats pour les atomes simples.

L'équation de Schrödinger a trois propriétés essentielles:

Elle fait intervenir de façon intrinsèque les nombres complexes [via le facteur i=√(-1)]. Partout ailleurs en physique, seuls les nombres réels interviennent, même s'il est parfois plus simple d'utiliser les nombres complexes comme intermédiaires de calcul (en électrodynamique par exemple, ou dans la physique des ondes). Schrödinger ne perçut d'ailleurs pas immédiatement cela et dans son premier article, il commence par laisser entendre que seule la partie réelle a un sens physique avant de conclure à la fin que la fonction ψ doit être "considérée comme essentiellement complexe".
Elle est linéaire dans la fonction ψ. Cela implique que si ψ₁ est une solution, il en est de même de aψ₁ (où a est un nombre complexe quelconque), et si ψ₂ est une autre solution, il en est de même de ψ₁+ψ₂. Cette linéarité (qui survit dans toutes les formes de la mécanique quantique) est à l'origine des "paradoxes" de la mécanique quantique.
C'est une équation différentielle du premier degré par rapport au temps: cela signfie que la connaissance de la fonction d'onde ψ(t₀) à un instant quelconque t₀ permet de la déterminer à tout instant t de manière univoque.

☛ L'équation d'évolution temporelle de la fonction d'onde est une équation déterministe, et Schrödinger espérait ainsi faire de la mécanique quantique une théorie aussi déterministe que la mécanique classique, les objets de son étude étant les ondes plutôt que des particules.

☛ une équation d'onde est une équation différentielle dont les solutions dépendent des conditions aux limites qui sont imposées. Ces solutions forment, dans de nombreuses circonstances, des ensembles discrets de solutions: par exemple, une corde vibrante ne vibre qu'à certaines fréquences précises (le fondamental et ses harmoniques). Il existe alors une étroite corrélation entre les paramètres de l'onde (fréquence et amplitude) et les conditions aux limites (taille du système par exemple), et cette corrélation s'exprime par des nombres entiers (par exemple, les fréquences de vibration sont des multiples entiers d'une fréquence fondamentale).

Les valeurs permises, comme les fréquences, sont les valeurs propres du problème, et les solutions (la fonction d'onde) sont des fonctions propres. La quantification se réduit au problème mathématique de trouver les fonctions propres et les valeurs propres de certaines équations différentielles auxquelles on fixe certaines conditions aux limites. Cela explique le titre de la série d'articles de Schrödinger : Quantisierung als Eigenwertproblem (La quantification comme problème de valeurs propres).

Équivalence entre mécanique des matrices et mécanique ondulatoire

Born, travaillant avec Wiener pendant l'hiver 1925-1926, avait perçu que les matrices carrées de l'approche de Heisenberg sont un cas particulier d'opérateurs linéaires dans un espace vectoriel. Schrödinger montra l'équivalence entre son approche ondulatoire et la mécanique des matrices dès mars 1926, ainsi que Pauli indépendamment (lettre du 12 avril à Jordan).

État (matrice-vecteur) ➛ fonction d'onde ψ(x,t)

Matrice carrée ➛ opérateur différentiel s'appliquant à une fonction, la fonction d'onde ψ(x,t)

Exemples

P_x ψ ➛ -iħ ∂ψ/∂x
Q_x ψ ➛ x ψ
H ψ ➛ -ħ²/2m ∂²ψ/∂x² + V ψ
L_z ψ ➛ –iħ (x∂ψ/∂y - y∂ψ/∂x)

Il y a une différence cependant entre les approches de Schrödinger et de Heisenberg: dans la première, la fonction d 'onde dépend du temps mais pas les opérateurs qui agissent sur elle, dans la seconde, ce sont les opérateurs (les matrices) qui dépendent du temps. Il est bien sûr possible d epasser d'une représentation à l'autre.

De l'onde à la fonction d'onde

Dans sa conférence Nobel de 1933, Schrödinger expliqua l'influence qu'avaient eu sur sa réflexion les idées d'Einstein et de de Broglie, et combien il lui semblait évident que matière et lumière devaient avoir un comportement similaire. Il y expliquait comment le principe de Fermat selon lequel la lumière suit le chemin le plus rapide, suffisait à retrouver toutes les lois de l'optique géométrique et le trajet (purement fictif) des rayons lumineux, sans devoir imaginer que ceux-ci soient des trajectoires de corpuscules. En mécanique classique, Lagrange puis Hamilton avaient réécrit la mécanique newtonienne en partant du principe de moindre action de Maupertuis, généralisant le principe de Fermat. Comme de Broglie, Schrödinger pensait que le parallèle entre lumière (Fermat) et matière (Maupertuis) pointait vers une description ondulatoire de la matière, description dans laquelle une (trajectoire de) particule serait aussi fictive qu'un rayon lumineux. Mais, disait Schrödinger, les billes ou les planètes ressemblant peu à des ondes, cette description ne parut jamais aller de soi.

Jusqu'à la mécanique quantique. Ce n'est qu'en acceptant une nature ondulatoire pour la matière, et donc les phénomènes caractéristiques de diffraction et d'interférence, qu'il devenait possible d'expliquer la quantification imposée par Bohr aux atomes par l'interférence des ondes de matière. Et comme ces phénomènes ne deviennent sensibles que pour des systèmes de dimension comparable à(ou plus petite que) la longueur d'onde, les effets quantiques disparaissent pour des échelles macroscopiques, donnant l'apparence d'un monde de particules. "En réalité, l'atome est simplement la diffraction d'une onde électronique capturée par le noyau de l'atome" dit Schrödinger, expliquant ainsi pourquoi la taille d'un atome est automatiquement comparable à la longueur d'onde de l'électron, la longueur de de Broglie, reliée au quantum d'action h qui apparaît aussi dans l'autre théorie ondulatoire, celle de la lumière.

espace ➛ espace de phase ➛ espace abstrait

Schrödinger proposait d'abandonner l'idée même de particule pour décrire un électron et de la remplacer par celle d'onde (de fonction d'onde plus exactement). Pour une seule particule, cette onde Ψ se déployait dans l'espace et il était relativement simple de se l'imaginer. Pour plusieurs particules c'était un peu plus difficile, mais encore possible. Selon Schrödinger, un électron n'était pas un objet quasi-ponctuel mais il remplissait tout l'espace avec une densité locale donnée par |Ψ|² = Ψ^*Ψ.

En effet, la densité ρ = |Ψ|² = Ψ^*Ψ obéissait à la classique équation de conservation ∂ρ/∂t + ∇.j = 0 en définissant de la manière habituelle par j = [Ψ^*∇Ψ – Ψ∇Ψ^*] h/2im . En multipliant ces quantités par la charge de l'électron e, cela pouvait s'interpréter comme une densité de charge électrique e|Ψ|² et un courant électrique ej. En les multipliant par la masse m de l'électron, cela devenait une densité de masse et un courant de matière.

Proposée dans son 4° article de la série Quantisierung als Eigenwertproblem en 1926, cette interprétation fut réfutée dès 1927 par Erwin Madelung (1881-1972) car les différentes parties de l'électron auraient alors dû interagir électromagnétiquement.

Interprétation probabiliste

Né en 1882 à Breslau (aujourd'hui Wrocław en Pologne), Max Born avait reçu une solide formation de mathématicien, d'abord à Breslau avec Jakob Rosanes, un spécialiste de géométrie algébrique qui (entre autres) lui enseigna l'algèbre des matrices, puis à Göttingen avec Herman Minkowski, David Hilbert (dont il fut le "scribe") et Félix Klein sous la direction de qui il passa son doctorat sur des questions d'élasticité. Il se tourna ensuite vers la physique et il fut assistant à Göttingen, puis à Berlin, avant de devenir professeur de physique mathématique à Göttingen en 1921, succédant à Peter Debye, et directeur du nouvel Institut de physique théorique. Il en profita pour obtenir un second poste pour James Franck, à la tête de l'Institut de physique expérimentale. Wolfgang Pauli fut brièvement son assistant, poste occupé à partir de 1923 par Heisenberg et Jordan.

Après avoir établi la mécanique des matrices sur une base mathématique solide, Born utilisa cependant la mécanique ondulatoire d'usage plus simple en apparence. Il défendit alors l'idée que la fonction d'onde n'était qu'une amplitude de probabilité, cocnept qui lui apporta le prix Nobel, mais pas avant 1954 (probablement parce qu'il était difficile de le récompenser pour son apport essentiel à la mécanique des matrices, pour laquelle Heisenberg avec déjà eu le prix Nobel, sans récompenser aussi Jordan devenu politiquement infréquentable.

Lors de l'arrivée au pouvoir d'Hitler, Born émigra, devenant professeur à Cambridge de 1933 à 1936, puis à Edinbourg de 1936 à 1953. Born était un enseignant remarquable, certains de ses ouvrages sont encore quotidiennement utilisés (le Born & Wolf d'optique par exemple), et le nombre de ses étudiants et collaborateurs devenus ensuite célèbres est impressionnant: outre Heisenberg et Jordan, il dirigea les thèses de Delbrück, Elsasser, Hund, Goeppert-Mayer, Nordheim, Oppenheimer et Weisskopf, et il eut pour assistants à Göttingen Pauli, Rosenfeld, Fermi, Teller et Wigner.

Born
Max Born (1882-1970)

Collisions de particules

Dans l'approche de Schrödinger, la fonction d'onde Ψ(x,t) d'une particule est une quantité qui dépend de la position x de la particule et du temps t. Schrödinger y voyait dans la fonction d'onde un étalement spatial de la particule décrite, qui était donc matériellement plutôt une onde qu'une particule. Mais Born ne partageait pas cet avis car les détecteurs enregistraient bien le passage, ou l'impact, de quelque chose de localisé, donc une particule: les scintillations sur un écran de sulfure de zinc, les cliquetis d'un compteur Geiger ou les trace photographiées dans une chambre à brouillard ne pouvaient pas s'interpréter comme quelque chose d'aussi diffus qu'une onde (la réponse de Schrôdinger était qu'il fallait en ce cas considérer des paquets d'onde). Born pensa que la question ne pouvait pas être tranchée en ne considérant que les électrons liés à un atome, et il se tourna vers les collisions entre particules.

Son idée était que l'intensité d'un flux de particules, des électrons par exemple, serait donnée par Ψ (ou|Ψ|²) aussi bien dans l'interprétation de Schrödinger (Ψ donne la densité locale d'une particule) que dans la sienne (Ψ donne la probabilité de présence d'une particule). Chaque électron arrivant sur une cible, un noyau atomique par exemple, engendrerait une onde secondaire partant de ce noyau avec une amplitude variant selon la direction. Si Schrödinger avait raison, chaque électron serait étalé tout autour du diffuseur. Si lui avait raison chaque électron serait détecté dans une direction unique, avec une probilité calculable.

Dès le printemps 1926, Born utilisa donc la mécanique ondulatoire de Schrödinger pour examiner le cas de la collision entre deux particules. Au départ, elles sont loin l'une de l'autre et elles peuvent être considérées comme des particules libres, non soumises à des forces. Puis elles s'approchent, interagissent, puis repartent au loin, à nouveau approximativement libres. Leur interaction est enregistrée par la modification de leur énergie et de leur impulsion (ce qui se traduit entre autres par un angle de déviation). Born aborda le problème pour une interaction relativement faible (ce qu'on appelle désormais l'approximation de Born) et il calcula la probabilité de déviation d'un électron par un noyau. Peu parès Wentzel retrouva de cette façon la formule de Rutherford pour la diffusion des particules alpha: Rutherford l'avait calculée classiquement, Wentzel montra qu'on la retrouvait en mécanique quantique.

Amplitude de probabilité

Dans son article sur les processus de collision (Zur Quantenmechanik der Stoßvorgänge, Sur la mécanique quantique des processus d'impact), suivi un mois après d'un second plus détaillé, Born interpréta la fonction d'onde comme une amplitude de probabilité, permettant de calculer la probabilitité de trouver la particule à la position x au temps t mais ne disant rien de sa répartition spatiale "réelle" avant sa détection hic et nunc.

L'idée était plus ou moins dans l'air, mais l'idée la plus souvent répandue était que la fonction d'onde était une probabilité. Mais Born montra que cette position était intenable, car une fonction d'onde est un nombre complexe avec une partie réelle et une partie imaginaire. or une probabilité doit être un nombre réel positif ou nul (inférieur à 1, mais il est toujours possible de renormaliser la fonction d'onde pour cela). D'autres avaient remarqué cette difficulté et ils avaient proposé de considérer comme une probabilité la norme |Ψ| de la fonction d'onde. Mais ce choix entre en conflit avec les propriétés des probabilités d'événements composés et Born montra qu'il était beaucoup plus cohérent d'interpréter comme une probabilité le carré de la norme |Ψ|² = Ψ^*Ψ (où Ψ^* est le complexe conjugué de Ψ).

Cette notion de probabilité, et surtout la perte de la causalité, conduisit à un accueil très réservé à ces idées. Born concluait en effet: "On n'obtient pas dans la théorie quantique de réponse à la question: Quel est l'état après la collision? mais seulement une réponse à la question Quelle est la probabilité d'un résultat donné après la collision. […] Du point de vue de notre mécanique quantique, il n'y a acune quantité (Grösze) qui détermine causalement l'effet de la collision pour un événement individuel. Devons-nous espérer découvirir plus tard une telle propriété […] et la déterminer dans les événements individuels? […] Pour ma part, je suis incliné à renoncer au déterminisme dans le monde atomique, mais ceci est une question philosophique à laquelle les arguments physiques seuls n'apportent pas de réponse." Dans son discours Nobel en 1954, Born expliqua que l'abandon d'un déterminisme absolu ne l'avait pas choqué parce que prédire l'état futur de n'importe quel système était de toute façon impossible si l'état initial n'était pas connu avec une précision absolue, ce qui est matériellement impossible, et que tout concept qui ne correspond à aucune observation réalisable ne devait avoir aucune place dans une théorie (cf. Einstein avec la relativité ou Heisenberg avec la mécanique des matrices).

Dans son deuxième article, Born rendait hommage à Einstein en disant que le point de départ des ses réflexions était une remarque d'Einstein concernant le champ électromagnétique de Maxwell et les quanta de lumière: Einstein "disait approximativement que l'onde n'est là que pour guider le quantum corpusculaire, et il parla en ce sens de champ fantôme (Gespensterfeld)". Einstein avait évoqué en effet un Führungsfeld, un champ pilote, dans ses commentaires des travaux de de Broglie (et la notion d'onde-pilote survécu très longtemps, dans l'approche de la mécanique quantique de David Bohm en particulier).

Pierre tombale de Born La plupart des physiciens se montrèrent très réticents face à l'abandon de la causalité, en particulier Schrödinger lui-même, qui déclara par la suite à plusieurs reprises que s'il avait imaginé les conséquences de sa théorie, il ne l'aurait sans doute pas publiée. Einstein se montra particulièrement hostile à l'idée de probabilité. C'est dans une lettre de réponse à Born, datée du 12 décembre 1926, qu'Einstein écrivit la phrase célèbre: "La mécanique quantique est très impressionnante. Mais une voix intérieure me dit que ce n'est pas encore la vraie réponse. La théorie nous apporte beaucoup mais ne nous rapproche guère des secrets du Vieux. Je suis entièrement convaincu qu'Il ne joue pas aux dés." Il reprit souvent cette expression, en particulier lors de discussions avec Bohr qui lui aurait répliqué "Ne dites pas à Dieu ce qu'il doit faire!".

Peu après que Born eut proposé son interprétation probabiliste de la fonction d'onde, cette idée fut renforcée par la découverte des inégalités de Heisenberg en 1927 qui contredisaient à la fois la notion de particules spatialement localisées et celle d'ondes de fréquence bien déterminée: l'image était plutôt celle d'une particule un peu étalée ou d'un paquet d'ondes un peu étalé en fréquence.

Max Born finit par recevoir le prix Nobel de physique en 1954 pour son interprétation probabiliste de la fonction d'onde, prix partagé avec Walther Bothe (pour son invention de la méthode des coïncidences).

Mais il considérait la relation de commutation comme sa contribution majeure à la science, et il la fit graver sur sa pierre tombale (comme Boltzmann fit graver son équation S=kLogW et Schrödinger la lettre Ψ).

La boîte de Pandore

Le penseur

L'interprétation de la fonction d'onde comme une densité de probabilité ouvrit une boîte de Pandore.

Contact