Alain Bouquet - Le noyau atomique

Attention: ces pages ne sont plus mises à jour car le site a déménagé. Il se trouve désormais à: cosmologie.wordpress.com Pensez à mettre à jour vos signets et bookmarks!

---

• Accueil
• Champs, noyaux et particules
• Cours et communication

---

Champs, Noyaux & particules

L'Antiquité

Atomisme moderne

Électrons

Radioactivité

• Rayons X et radioactivité
• Radioactivité: les Curie
• Radioactivité: Rutherford

Noyaux, protons et neutrons

• Noyau atomique: Rutherford
• Noyau atomique: Bohr, Soddy et Moseley
• Noyau atomique: Aston et Rutherford
• Neutron: Chadwick
• Neutron: Joliot-Curie
• Neutron: Fermi

Intruments, accélérateurs et détecteurs

Le photon

Mécanique quantique

• Mécanique ondulatoire
• Formalisme quantique
• Applications
• Théorie quantique des champs
• Électrodynamique quantique

Fission nucléaire

• Fission nucléaire
• Courses parallèles
• Manhattan
  • Les débuts
  • Réaction en chaîne
  • Hanford
  • Oak Ridge
  • Summer Study
  • Los Alamos
  • Hiroshima
• Réacteurs nucléaires

Fusion nucléaire

• Astrophysique nucléaire
• Armes nucléaires

Particules en tout genre

• Pions, kaons et étrangeté
• La voie octuple
• Quarks et leptons
• Symétries et champs de jauge
• Le "modèle standard"
• Grande unification et supersymétrie

Gravitation quantique?

• Les modèles d'atome avant Rutherford
• Encore les alphas
• Diffusion dans le modèle de Thomson
• Le modèle de Rutherford

Les modèles d'atome avant Rutherford

Les expériences de Thomson ne montraient pas réellement que des électrons étaient présents dans les atomes, ils pouvaient juste être produits au moment de leur émission. Cependant, le fait que le rapport q/m soit identique (aux erreurs de mesure près) quelque soit le matériau de la cathode, le gaz du tube, la haute tension appliqueé au tube, ou la vitesse des électrons, était compatible avec l'hypothèse des électrons dans l'atome. L'atome n'était donc pas le plus petit constituant de la matière.

La valeur du rapport q/m ~ 10¹¹ C/kg qu'il avait obtenu pour les rayons cathodiques était compatible avec la déduction de Lorentz à partir de l'éargissement des raies par effet Zeeman. On savait par ailleurs, à la suite des études d'électrochimie, que les ions avaient des rapports q/m très variés d'un électrolyte à un autre, mais toujours inférieurs à 10⁸ C/kg. Les chimistes s'étaient par ailleurs convaincus que les ions étaient des atomes ayant gagné ou perdu quelques unités d'une charge électrique élémentaire (l'électron de Stoney) et il était plausible que cette charge soit celle du corpuscule de Thomson, qu'on appela donc électron lui aussi. Par conséquent, l'électron avait probablement la même charge q que l'ion hydrogène (au signe près) mais un rapport q/m 1000 fois plus grand, et donc une masse 1000 fois plus petite (1836 fois avec l'amélioration des mesures).

Le plum-pudding de Thomson

Thomson se montra très audacieux: il supposa hardiment que tous les atomes étaient entièrement constitués de milliers d'électrons ("this matter being the substance from which the chemical elements are built up"). Comme ceux-ci possédaient une charge négative alors que les atomes étaient électriquement neutres (quand ils n'étaient pas ionisés), il fallait compenser leur charge par une composante d'électricité positive que Thomson imagina comme une sorte de gelée continue dans laquelle les électrons étaient enchâssés comme des prunes dans un cake: « the atoms of the elements consist of a number of negatively electrified corpuscles enclosed in a sphere of uniform positive electrification »

J.J. Thomson au Cavendish vers 1900

Thomson précisa son modèle en 1899, puis l'améliora en 1904: "I regard the atom as containing a large number of smaller bodies which I will call corpuscles, these corpuscles are equal to each other.... In the normal atom, this assemblage of corpuscles forms a system which is electrically neutral. Though the individual corpuscles behave like negative ions, yet when they are assembled in a neutral atom the negative effect is balanced by something which causes the space through which the corpuscles are spread to act as if it had a charge of positive electricity equal in amount to the sum of the negative charges of the corpuscles.... The detached corpuscles behave like negative ions, each carrying a constant negative charge which we shall call for brevity the unit charge; while the part of the atom left behind behaves like a positive ion with the unit positive charge and a mass large compared with that of the negative ion."

Représentation schématique du modèle de plum pudding de l'atome. Dans le modèle mathématique de Thomson, les «corpuscules» (les électrons modernes) sont placés de manière non-aléatoire, dans des anneaux tournants

En 1878, Alfred Mayer avait observé les figures d’équilibre d’aimants flottants:

Figures de Mayer:

Thomson s'en inspira en imaginant que les électrons pourraient de la même manière se répartir sur des coquilles, à peu près concentriques. Cela pourrait expliquer la présence des fréquences caractéristiques des raies spectrales? Distribution continue de la charge positive → pas d’instabilité radiative?

Les électrons (comme nous les connaissons aujourd'hui) étaient considérés comme dispersés au sein de l'atome, mais avec de multiples structures possibles pour leurs positionnements, comme en particulier des anneaux tournants d'électrons. Ces orbites étaient stabilisées dans le modèle par le fait que lorsqu'un électron se déplaçait loin du centre du nuage de matière positive, il serait « rattrapé » par une force d'attraction positive, car il y aurait plus de matériau de charge opposé dans son orbite. Dans le modèle de Thomson, les électrons sont libres de tourner dans des anneaux qui sont ensuite stabilisés par des interactions entre électrons, et les spectres devaient être considérés comme des différences d'énergies entre les différentes orbites des anneaux. J.J. Thomson tenta de prendre en compte dans son modèle les principales raies spectrales connues pour certains éléments, mais échoua. Wikipedia

Le grand chimiste Svante Arrhenius critiqua sévèrement le modèle de Thomson, d'abord parce qu'il n'avait aucune justification expérimentale, ensuite parce qu'il ne permettait (en l'état) aucune prédiction epérimentale, et enfin parce qu'il était invraisemblable qu'un atome contienne entre des milliers et des centaines de milliers d'électrons. Entre des éléments consécutifs du tableau périodique comme le sodium (11° élément, masse atomique 23), le magnésium (12° élément, masse atomique 24.3) et l'aluminium (13° élément, masse atomique 27) il devrait y avoir une différence respectivement de 2000 et 6000 électrons.

Thomson tint compte de ses critiques, d'autant qu'il devint peu à peu clair que le nombre d’électrons ne pouvait pas être aussi élevé, sans entrer en conflit avec

• les observations sur la diffusion de la lumière par les atomes : la variation de l’indice de réfraction d’un gaz avec la longueur d’onde de la lumière dépend de la masse M de la gelée posiitve, de la masse m et du nombre n des corpuscules, et les observations de Ketteler pour l’hydrogène montrent que M/(M+nm)/n ~ 1, d’où n ~ 1 et M >> m.
• les observations de Barkla sur la diffusion des rayons X montrant que, pour un gaz donné, le rapport entre l’énergie diffusée et l’énergie incidente était à peu près constante et proportionnelle à la densité du gaz. Cela permet à Thomson de montrer qu’il y a environ 25 corpuscules par molécule d’air (de poids atomique 29)
• l’absorption des rayons ß par la matière lui indiquant que le nombre de corpuscules était à peu près proportionnel à la masse atomique. Les résultats de Rutherford sur l’absorptionpar le cuivre et l’argent des ß émis par l’uranium lui donnèrent une constante de proportionnalité ~ 1.

Thomson conclut donc en 1906: "Le nombre de corpuscules dans l'atome est égal à son poids atomique".

La taille de l’atome dans le modèle de Thomson n’était pas précisée, et il n’y avait guère de moyen – dimensionnellement – de construire une longueur à partir des seules charge électrique e et masse me. La situation changea avec l’introduction de la constante de Planck h, et Bohr put construire une longueur a = h²/(m_e e²) = 0.053 nm, qu’il considéra comme le rayon de l’atome d’hydrogène (le « rayon de Bohr »).

Thomson pouvait inverser le problème et estimer la taille de son atome à partir des longueurs d'onde des raies spectrales (perdant ainsi la prédiction de ces longueurs d'onde). Supposons un électron déplacé de sa position d’équilibre de l’électron (a priori le centre de la distribution de charge positive? Ce déplacement entraîne une force de rappel proportionnelle au déplacement et donc un simple mouvement harmonique dont la fréquence ν(m,e,R) dépend de la masse m de l'électron, de sa charge e et du déplacement R (la seule inconnue du problème). Longueur d’onde λ ~ 500 nm → déplacement R ~ 10^-10 m → Ordre de grandeur correct.

Nagaoka: un modèle saturnien (1904)

Les anneaux de Saturne sont en équilibre car Saturne a une masse bien plus grande que ses anneaux. L'attraction gravitationnelle est en 1/r² comme l'attraction électrostatique → idée de Nagaoka Hantaro (1865-1950): une masse centrale lourde de charge positive, entourée d’électrons légers de charge négative → attraction électrostatique en 1/r² → stabilité de l'atome?

En fait non, car les électrons, d'une part se repoussent (alors que la matière des anneaux de Saturne s'attire), et surtout les électrons sont accélérés, comme n'importe quelle charge électrique, s'ils suivent des orbites circulaires ou elliptiques et rayonnent donc (brensstrahlung). Ils doivent donc rapidement perdre leur énergie et s'écraser sur la masse centrale. L emodèle de Nagaoka ne donne pas non plus d'explication à l'existance de raies spectrales.

Les dynamides de Lenard

Philip Lenard (1862-1947) et son côté obscur

L’absorption des rayons cathodiques (électrons) par la matière ne dépend que de la masse atomique de celle-ci (Über die Absorption der Kathodenstrahlen verschiedener Geschwindigkeit 1903) ⇒ les atomes sont tous formés des mêmes constituants, les dynamides, mais en nombre variable

Dynamides de Lenard pour l'hélium

Explique les électrons, l’ionisation, certaines régularités

Difficultés: liaison des dynamides, composante positive? raies spectrales?

Autres tentatives

Rayleigh

Lord Rayleigh (1906) : deux fluides, positif et négatif (approximation d’un grand nombre d’électrons)

Jeans

James Jeans (1906) : électrons vibrants

Stark

Johannes Stark (1910): archions (charge positive massive) soumis à une attraction magnétique et une répulsion électrique (compensée par des électrons)

Et beaucoup d’autres ! Enfin Rutherford vint…

Encore les alphas

Rutherford a toujours adoré bombarder des atomes avec des particules alpha. Dès 1906, il plaçait sur leur trajet des feuilles très minces (0.4 µm pour les feuilles d'or) pour éviter une trop forte absoption des alphas. Il observa l'élargissement d'un faisceau très étroit (Rutherford, Phil. Mag. vol. 12, p. 143, 1906). Rien de très surprenant en soi, les charges électriques des atomes devaient dévier les alphas (attirés par les électrons, repoussés par une distribution de charges positives, la « gelée » positive de Thomson ou autre chose). De plus des interactions multiples étaient à prévoir. Les images photographiques des impacts des α déviés par un champ électromagnétique étaient également légèrement floues, et Rutherford se demanda quelle était l'origine de ces déviations (ricochets sur les parois du montage, diffraction du faisceau, ou autre chose?).

Hans Geiger

Nommé professeur à Manchester en 1907, Rutherford lança une étude systématique de ces déviations parasites. Pour compter individuellement les alphas, Rutherford reprit l'idée d'un écran recouvert de sulfure de zinc qui émettait une brève scintillation quand un alpha la frappait (c'est ce que Crookes avait employé dans son spinthariscope). Ces scintillations étaient peu brillantes et pour les observer, il fallait accoutumer son regard à l'obscurité et cela nécessitait que l'observateur demeure dans le noir le plus total pendant toute la durée d'observation, ce qui pouvait prendre des heures. Rutherford confia cette tâche à Hans Geiger (1882-1945), venu le rejoindre après sa thèse à Erlangen en 1906. Geiger allait rester 5 ans avec Rutherford, années pendant lesquelles, en dehors de le conduire vers l'idée de noyau atomique, il allait établir en 1911 avec John Nuttall la corrélation entre le nombre des alphas émis (par unité de temps) par un élément radioactif et l'énergie de ces alphas. Cette loi de Geiger-Nuttall fut essentielle à George Gamow en 1928 pour expliquer l'émission d'une particule alpha comme un effet tunnel quantique. Mais Geiger réalisa aussi à Manchester, avec Rutherford, le premier exemple de compteur électrique enregistrant le passage d'une particule ionisante, qu'il améliora ensuite en 1928 avec W. Müller (le compteur de Geiger-Müller). Un tel instrument évitait la tâche fastidieuse de compter des scintillations dans l'obscurité avec tous les risques d'erreurs et de biais que cela comportait, mais il n'était pas encore très au point en 1908.

Hans Geiger et Ernest Rutherford en 1908 à Manchester © AIP

Rutherford avait noté qu'un faisceau de particules alpha traversant l'ouverture étroite d'un collimateur s'élargissait en traversant une mince feuille de métal ou une fenêtre de mica, et il demanda à Geiger de mesurer cet élargissement de manière plus quantitative, en comptant le nombre de particules alpha diffusé selon un angle donné. Geiger observa que le nombre de particules alpha diminuait très vite quand on s'écartait de la direction initiale (autrement dit, la diffusion était assez faible) et que l'immense majorité était déviée de moins de 1°. Qualitativement, c'était tout à fait ce à quoi Rutherford s'attendait puisque les particules alpha étaient plutôt massives et animées de grandes vitesses (~10 000 km/ soit 1/30 de la vitesse de la lumière) et que la plupart traverseraient la feuille métallique en n'étant qu'à peine déviées par les atomes rencontrés, un peu comme une balle de fusil traversant une planche de bois. Quantitativement, les résultats étaient moins satisfaisants car des alphas étaient parfois observés à des angles supérieurs à 1°, et Geiger et Rutherford blamèrent les diffusions parasites.

Montage de Geiger en 1908: R est la source des alphas (du radon 222, du radium A = polonium 218, ou du radium C = bismuth 214), S est une feuille métallique mince, Z l'écran de sulfure de zinc observée à travers le microscope M.

Geiger examina si l'effet dépendait de la nature de la feuille métallique en plaçant des feuilles d'aluminium, d'étain, d'argent ou de cuivre, et en variant l'épaisseur de ces feuilles. Il observa que l'angle de déviation augmentait avec l'épaisseur de la feuille, ce qui était cohérent avec l'idée que les particules alpha avaient plus de chance de subir plusieurs diffusions successives si elles rencontraient plus d'atomes au cours de leur progression à travers la feuille. L'angle de déviation augmentait également avec la masse atomique des atomes déflecteurs, les particules alpha étant plus déviées par une feuille d'or que par une feuille d'étain, et plus par une feuille d'étain que par une feuille de cuivre ou d'aluminium.

La déviation variait à peu près comme la racine carrée de l'épaisseur de la feuille et comme la racine carrée de la masse atomique du métal utilisé (H. Geiger, Roy. Soc. Proc. A, vol. 81, p. 174,1908).

L'expérience de Geiger et Marsden

L'étude de la diffusion des particules alpha devenait peu à peu un sujet d'étude à part entière, et Geiger suggéra en 1909 que cela pourrait constituer un bon sujet de thèse pour Ernest Marsden qui venait de rejoindre l'équipe. Marsden (1889-1970) était alors étudiant à l'université de Manchester et passionné par la radioactivité. Il devint ensuite professeur en Nouvelle-Zélande, sur la recommendation de Rutherford, et il eut également d'importantes responsabilités dans l'administration de la science. Assisté par Marsden, Geiger reprit l'étude de la diffusion de particules α par des feuilles d'or en se focalisant sur les diffusions à grand angle. Comme elles étaient rares, ils utilisèrent une source très intense, et le montage fut modifié pour observer la diffusion à tout angle. Le long tube fut remplacé par un tube court, source, collimateur et feuille métallique étaient solidaires et pouvaient pivoter autour du microscope:

Geiger et Marsden observèrent les diffusions par des feuilles de différentes épaisseurs, et des métaux allant de l'aluminium au plomb en passant par l'or dont des feuilles très minces pouvaient être superposées (et fixées à des plaques de verre pour en assurer la rigidité). Ils mesurèrent ainsi la décroissance du nombre d'alphas quand l'angle de diffusion augmentait. Rutherford demanda jusqu'à quel angle étaient observés des alphas. La réponse fut ahurissante: des alphas étaient observés à plus de 90°, donc du côté de la direction d'arrivée comme s'ils avaient rebondi sur la feuille. Ce phénomène avait été observé quelques années plus tôt pour les rayons bêta: il fut d'abord attribué à des bêtas secondaires, avant qu'il soit expliqué par une succession de diffusion des bêtas par les atomes. Mais les bêta sont des électrons, très légers, tandis que les alphas sont 8000 fois plus lourds. Selon la métaphore de Rutherford, racontant l'événement quelques années plus tard, c'était aussi extraordinaire que de tirer un obus de 380 mm sur une feuille de papier et de le voir rebondir!

Ces rebonds n'étaient pas fréquents, un alpha sur 20 000 d'après l'estimation de Marsden, mais c'était cependant énorme par rapport à ce qui était attendu. Geiger et Marsden les attribuèrent d'abord à des rétrodiffusions sur les parois et ils installèrent des blindages pour absober les alphas qui frappaient les parois. Mais l'effet persistait, et il dépendait du matériau de la feuille (1/8000 pour le platine, 1/20000 pour l'or). Ils montrèrent aussi que les alphas étaient renvoyés même par une faible épaisseur de matière, et qu'ils perdaient peu d'énergie dans cette opération. Ces deux points suggéraient que les alphas avaient interagi avec un très petit nombre d'atomes, mais l'ampleur de la déviation ne s'expliquait pas.

Schéma de principe de l'expérience de Geiger et Marsden.

Geiger et Marsden publièrent alors leur découverte, laissant à d'autres le soin de l'expliquer (Geiger & Marsden Proc. Roy. Soc. A vol. 82, p. 495-500, 1909).

Diffusion dans le modèle de Thomson

Pour comprendre pourquoi les diffusions à grand angle dans l'expérience de Geiger et Marsden étaient inexplicables dans le modèle de l'atome élaboré par J.J. Thomson (le seul modèle existant alors qui permettait des évaluations quantitatives), il faut revenir sur la diffusion de charges électriques les unes par les autres.

Déviation d’une charge électrique ponctuelle par une autre

Le problème de la diffusion d'une charge q₁ ponctuelle par une autre charge q₂, également ponctuelle donne lieu aux mêmes équations que celles résolues par Newton pour l'attraction entre deux masses ponctuelles, pour des charges de signe opposé (d'où attraction) et à des équations très voisines pour des charges de même signe (d'où répulsion). Si les charges ne sont pas ponctuelles, ce qui est bien sûr le cas dans le modèle d'atome proposé par Thomson, le calcul n'est pas modifié aussi longtemps que les deux distributions de charge sont 1) à symétrie sphérique et 2) restent extérieures l'une à l'autre (la même situation se présente aussi pour la gravitation).

Dans le cas où l'une des charges (=le diffuseur) a une masse beaucoup plus grande que l'autre, on a intérêt à décrire la diffusion du point de vue du diffuseur, et lla solution est que l'angle de déviation θ de la particule diffusée est proportionnel:

• aux charges q₁ et q₂ (plus les charges sont grandes, plus les forces sont élevées et plus la déviation est forte)
• à l'inverse du paramètre d'impact b, qui la distance à laquelle e diffusé passerait du diffuseur si aucune force n'agissait (si les charges passent loin l'une de l'autre, elles s'infleuencent peu)
• à l'inverse de la masse M de la particule diffusée (si elle est massive, à charges données, son accélération par le diffuseur sera faible et donc sa déviation)
• et à l'inverse du carré de la vitesse V de la particule diffusée (si elle est très rapide, sa déviation sera plus faible)

Soit tan(θ/2) = q₁ q₂ / [b M V²] . Pour de petits angles de diffusion, tan(θ/2)~θ/ 2, et cet angle est le rapport des énergies potentielle (q₁q₂/b) et cinétique (MV²/2).

Si le paramètre d'impact b est très petit (ce qui conduit à un impact frontal), l'angle de diffusion → π (autrement dit le projectile repart en arrière, après s'être approché de la cible jusqu'à ce que sa vitesse devienne nulle). Dans le cas d'une attraction (gravitationnelle ou électrostatique), la trajectoire suivie est une ellipse (pensons aux planètes), une parabole ou une hyperbole selon la vitesse transversale initiale (par conservation du moment angulaire). Dans le cas d'une répulsion, la trajectoire est hyperbolique (mais il n'est pas possible, en observant une trajectoire hyperbolique, si l'on a affaire à une attraction ou une répulsion).

La difficulté rencontrée par Rutherford et ses collaborateurs était quantitative. Dans le cas de la diffusion d'une particule alpha par un atome d'or, les quantités en jeu sont:

• charge élémentaire e = 1,6x10^-19C ⇒ q₁ = 2e et q₂ = Ze, avec Z=79 pour l’or (cette valeur était surestimée à l'époque en l'absence d'identification entre le numéro atomique, c'est-à-dire le rang dans le tableau de Mendeleiev, et la charge électrique Z, ce qui ne fut fait qu'en 1913 à la suite des travaux de Moseley, cf. infra) et la valeur de la charge élémentaire elle-même était encore imprécise.
• unité de masse atomique m = 1.67x10^-27kg (valeur alors très incertaine également, faute de mesure précise du nombre d'Avogadro) et M = 4m pour une particule alpha (3.73 plus précisément).
• vitesse des alphas V de 10⁷ m/s à 2*10⁷ m/s selon la source des alphas (par exemple avec une source de radon 222, l'alpha a une énergie de 5.59 MeV et donc une vitesse de 1.6*10⁷ m/s).
• dans le système international d'unités (charges en coulombs, masses en kilos, distances en mètres…), il y a un facteur k=8.987*10⁹ Nm²/C² devant l'équation précédente.

En prenant pour paramètre d’impact b une distance de 1 Å (de l'ordre du rayon d'un atome d'or, 1.35 Å = 1.35*10^-10 m), une vitesse V=10⁷ m/s et Z~100, la formule précédente prédit une déviation θ de l'ordre de 1.4*10^-3 radians, soit 0.08° ou 5'.

Le paramètre d'impact est la seule quantité sur laquelle on puisse jouer, et on n'obtient une déviation proche de 1° que si la particule alpha passe à 0.04 Å du centre de l'atome. Mais si l'atome a vraiment la structure interne supposée par le modèle de Thomson, le calcul précédent n'est pas valable quand la particule alpha passe à l'intérieur de l'atome, car la charge du diffuseur ne peut plus être supposée ponctuelle. D'autre part, la probabilité que (le centre de) la particule alpha passe en un point de la feuille d'or peut être supposée uniforme (dans la petite zone touchée par le faisceau collimaté), ce qui permet de calculer la probabilité qu'elle passe à une distance b du centre d'un atome diffuseur et de là la probabilité que son angle de diffusion soit θ. On peut montrer dans ces conditions que cette probabilité P(θ) ∝ 1/θ⁴ . Elle décroît donc très vite quand l'angle θ augmente, et il est donc très rare de trouver des angles de déviation très supérieurs à 1°.

Diffusion d’un alpha par un atome de Thomson

Dans le modèle de Thomson, un atome est une sphère de « gelée » d'électricité positive ayant un rayon de quelques Ångströms, qui contient aussi l'essentiel de la masse de l'atome, et dans laquelle sont enfouis des électrons. Ceux-ci ne jouent pas de rôle important dans la diffusion des alphas du fait de leur faible masse. Rutherford ne réalisa d'ailleurs pas cela immédiatement et il se lança inutilement dans des calculs plus compliqués que nécessaire. Les alphas, étant des ions d'hélium, sont également envisagés comme de petites sphères d'électricité positive, sans électrons (l'ion a perdu les deux électrons de l'atome) et très probablement bien plus petite que celle d'un atome d'or bien plus lourd. Cela suppose implicitement que la gelée est la même pour tous les atomes, mais en quantité plus ou moins proportionnelle à la masse de l'atome. La diffusion ressemblerait donc à ceci:

Mais tout se passe comme si les charges étaient ponctuelles tant qu'elles ne se pénètrent pas. Dans le cas où les deux charges ne font que se frôler, on retrouve la diffusion par des charges ponctuelles et un angle de diffusion moyen de 0.04°.

Quand la particule alpha pénètre plus en profondeur dans un atome d'or, elle n’est sensible qu’à la charge électrique qui se trouve à l’intérieur de sa trajectoire (entre elle et le centre de la « gelée »), la charge qui se trouve à l'extérieur se compensant en grande partie par symétrie. Supposons la densité de charge constante. Quoique injustifiée a priori, cette hypothèse est la plus simple, et peut être abandonnée par la suite si les prédictions se révèlent fausses. La charge à l'intérieur du rayon b (le paramètre d'impact) est alors proportionnelle au volume, donc au cube du rayon, et donc égale à Ze(b/R)³, où R est le rayon de l'atome. Cette charge est beaucoup plus faible que la charge totale Ze de l'atome, et elle se comporte encore comme si elle était ponctuelle.

L'angle de déviation θ ~ 2q₁q₂/[bMV²] = 2e Ze(b/R)³/[b M V²] est donc maintenant proportionnel au carré du paramètre d'impact b. Il devient donc beaucoup plus petit qu'avant (pour un paramètre d’impact b ~ 0.04 Å il est inférieur à 10^-6 radians ce qui est négligeable). Bien sûr, rien n’indique que la densité de la «gelée» soit constante, mais la seule façon d'augmenter l'angle de diffusion est d'augmenter fortement la densité de charge près du centre, et c'est précisément ce à quoi Rutherford finit pas se résoudre.

Mais auparavant, il fallait examiner si, lors de la traversée d'une feuille d'or (ou d'un autre métal), la particule alpha ne subissait pas plusieurs diffusions successives dont les angles de déviation, se cumulant, la conduisaient peut-être à ressortir à grand angle:

Déviations successives d'une particule alpha à la traversée d'une feuille d'or: l'angle de déviation est important (quoique < 1°) quand la particule passe à peu près à mi-distance entre deux atomes, et beaucoup plus faible quand elle passe près du centre d'un atome.

Les feuilles d'or employées avaient des épaisseurs de 0.2 µm, ce qui correspond à un millier d'atomes d'épaisseur. Chaque déviation est, au mieux, de 0.08°, et d'un atome au suivant elle peut se faire aussi bien dans un sens que dans l'autre. Cela équivaut donc à un problème de marche au hasard avec 1000 pas successifs de 0.08° chacun. Une telle marche conduit à s'écarter -en moyenne- de son point de départ de la longueur d'un pas multiplié par la racine carrée du nombre de pas, donc ici de 0.08°*√(1000) = 2.4°. Ceci surestime la déviation car, dans ce modèle, les diffusions qui passent près du centre d'un atome sont inefficaces.

On peut donc de comprendre que l'angle moyen de diffusion soit de l'ordre du degré, mais absolument pas comment il peut atteindre 90°, voire même plus. Un calcul plus soigné changerait certainement les valeurs obtenues, mais pas de plus qu'un facteur 2 ou 3. D'où le problème auquel se heurtait Rutherford. Il est bien sûr permis de penser qu'une série de diffusions sur les atomes pourrait, par le plus grand des hasards, se faire toujours dans le même sens. Après tout, 1000 diffusions de O.08° dans le même sens aboutissent à une déviation 80°. On approche des 90°… mais la probabilité d'un tel événement est la même que celle d'obtenir 1000 fois "pile" successivement en lançant une piéce de monnaie, qui est de (1/2)¹⁰⁰⁰~10^-300, considérablement plus petite que les 1/10000 observés par Marsden.

Le modèle de Rutherford

Un cheminement difficile

Rutherford mit presque deux ans à trouver la solution. Geiger et Marsden avaient découvert la diffusion à grand angle des alphas en mars-avril 1909. En septembre 1909, Rutherford exposait lors d'une conférence sa surprise que des collisions multiples parviennent à renvoyer en arrière une particule alpha, et il en déduisait que l'intensité de forces électriques dans un atome étaient peut-être plus intenses qu'on ne l'imaginait. Geiger et Marsden avaient continué entre temps leurs mesures (elles se pousuivirent jusqu'en 1913), et Geiger put annoncer en février 1910 que l'angle moyen de déviation était de l'ordre de 1°, mais il précisait dans l'article qu'aucune explication n'était encore envisageable. En mars, puis en juin et en décembre 1910, J.D. Crowther (qui était un étudiant de J.J. Thomson) présenta un modèle pour la rétrodiffusion des bêtas en termes de collisions multiples sur les atomes, mais Rutherford se rendit compte que la même explication ne pouvait s'appliquer aux alphas en raison de leur masse plus élevée.

Il repensa (peut-être) à ce moment aux résultats de Geiger et Marsden qui montraient que la rétrodiffusion des alphas se faisait sur une faible épaisseur, une centaine d'atomes au plus, et que leur perte d'énergie était minime. Cela pointait vers un très petit nombre de rencontres entre un alpha et les atomes d'or avant que l'alpha ne ressorte, peut-être même une rencontre unique! Il se lança dans une série de calculs à la fin de l'année 1910 (ils les mentionne à cette époque, sans donner de détails, dans plusieurs lettres à des collègues). Rutherford résumait les résultats de Geiger et Marsden de la manière suivante:

1. la plupart des particules alpha traversent la feuille d'or sans interagir, et arrivent droit sur le détecteur, l'écran au sulfure de zinc (la largeur du faisceau traversant le collimateur expliquant la largeur de la zone d'impact)
2. un petite fraction des particules interagit avec les atomes d'or, qui les dévient d'une fraction de degré chacun (d'où une déviation moyenne de 0.87° dit Rutherford)
3. une minuscule fraction (entre 1 sur 8000 et une sur 20000 selon le métal rencontré) est déviée de plus de 90°

Rutherford tâtonna longtemps. Il envisagea de nombreuses possibilités:

• que les particules alphas ne soient pas diffusées par les atomes d'or individuellement, mais par l'ensemble du réseau atomique de l'or;
• qu'elles soient diffusées par des électrons extrêmement rapides (mais pour qu'une particule alpha soit renvoyée vers l'arrière, elle devait diffuser sur quelque chose de masse au moins égale à elle même, par conservation de l'impulsion);
• que des forces non-électriques soient en jeu (après tout la production même des particules alphas, et la radioactivité de façon plus générale, semblaient difficiles à expliquer par l'électromagnétisme maxwellien);
• que l'énergie ou l'impulsion ne soient pas conservés à l'échelle atomique, mais seulement en moyenne quand un grand nombre d'atomes étaient en jeu (idée souvent reprise dans les années suivantes, en particulier pour expliquer la transmutation bêta);
• et sans doute bien d'autres dont il n'a pas laissé de traces.

En admettant que la diffusion des alphas soit due à des forces électromagnétiques, quelle distribution de charges électriques pouvait en être responsable? La neutralité électrique des atomes imposait la présence de charges électriques positives pour compenser les charges électriques négatives des électrons. Le nombre d'électrons dans un atome était encore très incertain, mais il semblait être du même ordre de grandeur que la masse atomique (Moseley allait montrer en 1913 qu'il était égal au numéro atomique, soit à peu près la moitié de la masse atomique). Les charges positives compensatrices ne pouvaient pas former une gelée continue comme le supposait Thomson, car cela excluerait la possibilité des diffusions observées à grand angle. Donc elles devaient former des grumeaux compacts, de taille nettement inférieure à la taille de l'atome, et de masse nettement supérieure à la masse d'une particule alpha pour permettre des ricochets vers l'arrière. Quelques années plus tôt, Philip Lenard avait observé que les rayons cathodiques (électrons) parcouraient de grandes distances dans les gaz, et il en avait déduit que les atomes étaient en grande partie vides. Rutherford convergea alors peu à peu vers l'idée que toute la charge positive était peut-être concentrée en un seul grumeau, concentrant donc également toute la masse de l'atome (celle des électrons étant négligeable) et dès lors situé au centre même de l'atome, et entourée d'un essaim d'électrons.

Feuille de calculs de Rutherford lors de la découverte du noyau: le schéma en haut à droite montre encore les électrons dont Rutherford essayait de calculer l'effet sur la diffusion des alphas, et la concentration de charge Ze marquée par une croix au centre de l'atome. Le schéma plus bas esquisse le trajet de la particule alpha dans l'atome.

Pour rendre compte aussi bien des diffusions à petit angle que des diffusions à grand angle, l'explication de Rutherford fut que la charge électrique de l'atome devait être extrêmement concentrée. Concentrée à quel point? L'équation θ = 2q₁q₂/[bMV²] donnant l'angle de diffusion θ en fonction du paramète d'impact b pour des charges ponctuelles apportait la réponse. Dans le cas de l'or, on avait θ ~ 0.08°*[1Å/b]. Pour avoir une déviation de 180°, il fallait donc que la charge positive de l'atome soit contenue à l'intérieur d'un rayon au moins 2000 fois plus petit que la taille de l'atome (1Å=10^-10m). D'où la conclusion de Rutherford en 1911 : "Nous supposerons que, pour des distances inférieures à 10^-14m, la charge centrale de même que celle de la particule alpha sont concentrées en un point." Dans ce cas, la trajectoire est hyperbolique:

Figure de l'article de Rutherford en 1911 explicitant son modèle de concentration de charge et la trajectoire hyperbolique résultante.

Timbre en l'honneur de Rutherford, illustré par la déviation des particules alpha

C'est ce nous appelons aujourd'hui le noyau de l'atome, mais Rutherford n'emploie alors que le mot "concentration de charge". Dans un livre publié en 1912, il n'emploie qu'une seule fois le mot "noyau". Cette idée d'un noyau compact rend compte des observations par Geiger et Marsden:

1. le noyau est si petit que la plupart des particules alpha passent trop loin de lui pour être déviées de façon mesurable;
2. certaines passent cependant suffisamment près (~10^-11m) pour être déviées d'une fraction de degré;
3. un nombre plus restreint passe encore plus près et sont déviées de 1°;
4. quelques très rares particules parviennent à approcher de si près du noyau (~10^-14m) qu'elles sont violemment déviées à des angles de plusieurs dizaines de degrés.

Rutherford présenta ses résultats le 7 mars 1911 au Cavendish puis il envoya un article détaillé "The scattering of alpha and beta particles by matter and the structure of the atom" (Philosophical Magazine 21-669, 1911). Il donnait le détail des calculs et la formule (aujoud'hui formule de Rutherford) permettant d'estimer la distribution des angles de déviation en fonction de l'énergie des particules alpha (variant selon la source d'alphas employés) et en fonction de la charge électrique positive Ze de l'atome sur lequel elles diffusaient.

Le calcul de Rutherford

Supposant donc ponctuelles aussi bien la charge de la particule alpha que celle du noyau cible, Rutherford montra que la particule alpha suivait une trajectoire hyperbolique:

De la relation entre paramètre d'impact b et angle de diffusion θ, Rutherford put calculer combien de particules étaient déviées d'un angle entre θ et θ+dθ (celles qui passent dans la couronne entre b et b+db):

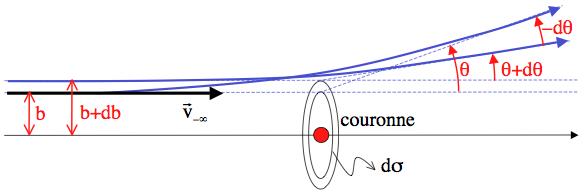
L'étape suivante est de calculer combien de particules sont ainsi diffusées dans la direction θ (à dθ près) quand N particules bombardent une cible mince contenant n noyaux par unité de surface,ce qu'on appelera plus tard une "section efficace de diffusion". on aboutit ainsi à la "formule de diffusion de Rutherford":

dN/dθ = N n [k Ze²/MV²]² 2πsin(θ)/sin⁴(θ/2)

ou, en fonction de l'angle solide Ω (dΩ= 2πsin(θ))

dN/dΩ = N n [k Ze²/MV²]² /sin⁴(θ/2)

Rutherford montrait également que la diffusion des particules alpha ne changeait pratiquement pas leur vitesse (quelques pour cent au plus), essentiellement parce qu'elle sont bien plus légères que les noyaux étudiés: un transfert d'énergie lors d'une collision n'est efficace que si les deux objets entrant en collision ont des masses voisines. Il spécula alors sur ce qui se passerait si les particules alpha entraient en collision avec des atomes très légers, l'hydrogène par exemple, mais aucune expérience de ce genre n'avait encore eu lieu. Rutherford remarquait cependant que le ralentissement étant plus marqué avec des atomes légers comme l'aluminium (~10%), et la pénétration dans l'air des particules alpha variant empiriquement comme le cube de leur vitesse, ce ralentissement devrait être observable.

Rutherford calcula ensuite la probabilité qu'une déviation d'un angle θ donné résulte d'une seule diffusion ou de plusieurs diffusions d'angles plus petits, et il montra que la probabilité d'une diffusion unique était toujours supérieure à celle d'une diffusion multiple, et que l'écart augmentait rapidement avec l'angle θ de diffusion. Par conséquent, les diffusions multiples ne jouent qu'un rôle mineur à petit angle, et sont totalement négligeables à grand angle. Rutherford examina finalement la possibilité que la charge électrique positive de l'atome soit en fait répartie dans un (très) petit volume, et non ponctuelle, éventuellement sous la forme de plusieurs composantes, mais conclut que les données étaient trop incertaines pour trancher la question. Il nota la ressemblance de son modèle avec celui de Nagaoka, mais essentiellement comme argument en faveur de la stabilité du modèle.

À partir des données rassemblées par Geiger et Marsden, et des expériences de Crowther sur la diffusion des électrons (particules bêta), Rutherford put ainsi donner dans cet article ses estimations des valeurs de Z pour les atomes employés, et il trouva qu'elles augmentaient avec la masse atomique de l'élément, ce qui parut cohérent. Par contre ses estimations étaient systématiquement trop élevées, pour une raison non élucidée:

• Z(Au) : entre 97 et 114 (au lieu de 79)
• Z(Al) : 22 (au lieu de 13)
• Z(Cu) : 42 (au lieu de 29)
• Z(Ag) : 78 (au lieu de 47)
• Z(Pt) : 138 (au lieu de 78)

Le prédictions du modèle de Rutherford, en particulier la dépendance explicite de la distribution angulaire en Z²/sin⁴(θ/2), furent confirmées par Geiger et Marsden qui effectuèrent entre 1912 et 1913 des mesures très précises de la déviation des alphas. Une expérience de diffusion ne permet pas de savoir si on est dans la situation où les charges se repoussent (même signe) ou s'attirent (signes opposés), mais Rutherford a naturellement supposé être dans le premier cas, puisqu'il diffusait des noyaux d'hélium sur des noyaux d'or.

A posteriori, que la formule de Rutherford donne les bons résultats est (presque) un heureux hasard, dan sla mesure où le calcul de Rutherford est, par la force des choses, entièrement classique. Mais le calcul analogue en mécanique quantique donne le même résultat (essentiellement en raison du potentiel électrique en 1/r). Si le modèle d'atome de Thomson avait été le bon, le calcul quantique aurait donné un résultat très différent du calcul classique.

Un intérêt poli

Aussi spectaculaire qu'apparaisse aujourd'hui l'affirmation par Rutherford de l'existence d'un noyau atomique, elle ne suscita sur le moment qu'un intérêt poli. Elle ne fut pas du tout mentionnée lors de la première conférence Solvay de 1911, quelques mois plus tard, et à peine signalée lors de la deuxième en 1913 (alors que ses prédictions avaient entre temps été vérifiées par les mesures plus précises de Geiger et Marsden).

Cette deuxième conférence Solvay était consacrée à "La structure de la matière", et J.J. Thomson présenta le rapport de synthèse sur la structure de l'atome. Thomson fit à peine référence aux résultats de Rutherford sur le noyau et, en les mentionnant à la fin, il soutint l'idée que les déviations à grand angle seraient dues à des "forces spéciales", non-électriques, et il rejetait l'idée de noyau compact:

Rutherford lui-même ne sembla pas avoir pris immédiatement conscience de l'importance de sa découverte: dans la réédition en 1912 de son traité de radioactivité, il mentionne à peine le noyau, alors qu'il figure de façon bien plus centrale en 1914 après les travaux de Bohr et de Moseley. En 1912, Rutherford pensait encore que si les alphas venaient du noyau, les bêtas et gammas venaient d'une instabilité des électrons entourant le noyau. C'est Bohr qui conclut en 1913 que tous venaient du noyau.

Contact