Alain Bouquet - Le modèle standard
Attention: ces pages ne sont plus mises à jour car le site a déménagé. Il se trouve désormais à: Pensez à mettre à jour vos signets et bookmarks! |
Champs, Noyaux & particules
Radioactivité
Noyaux, protons et neutrons
- Noyau atomique: Rutherford
- Noyau atomique: Bohr, Soddy et Moseley
- Noyau atomique: Aston et Rutherford
- Neutron: Chadwick
- Neutron: Joliot-Curie
- Neutron: Fermi
Intruments, accélérateurs et détecteurs
Mécanique quantique
- Mécanique ondulatoire
- Formalisme quantique
- Applications
- Théorie quantique des champs
- Électrodynamique quantique
Fission nucléaire
Fusion nucléaire
Particules en tout genre
- La révolution de novembre
- L'observation des bosons W et Z
- LEP
- LHC
- Le modèle standard
- Interaction forte
- Interaction électrofaible
La révolution de novembre
Un quatrième quark ?
Expérimentalement K0 ⇏ µ+µ– alors que c’est théoriquement possible via

Glashow, Iliopoulos et Maiani 1970 : un quatrième quark compenserait (presque) exactement ce diagramme par cet autre

Autre motivation : Adler, ainsi que Bell et Jackiw, avaient montré en 1969 que certaines symétries du lagrangien pouvaient être brisées par les corrections radiatives
Cette « anomalie » était proportionnelle à la somme des charges des fermions
- électron + neutrino + (quark u + quark d)*3 = -1 + 0 + (2/3–1/3)*3 = 0
- muon + neutrino + (quark c + quark s)*3 = -1 + 0 + (2/3–1/3)*3 = 0
- les facteurs 3 venant des 3 couleurs
➡ la compensation de l’anomalie exigeait un quark de charge 2/3
Après la découverte du lepton tau (1975), il fallut rechercher un quark bottom (1977) puis un quark top (1995) pour la même raison.
Le rapport R = σ(e+e– ➛ hadrons)/σ(e+e– ➛ µ+µ–)
Réaction e+e–➛µ+µ– au 1° ordre

➡ amplitude e2 M [élément de matrice M incluant la cinématique]
➡ section efficace σ(e+e– ➛ µ+µ–) = e4 |M|2
Les hadrons sont formés de quarks ⇒ l'amplitude de diffusion est proportionnelle aux charges Q des quarks concernés
Réaction e+e–➛qq au 1° ordre

➡ amplitude Qe2 M
[Q = 2/3 pour le quark u, Q = –1/3 pour d et s]
➡ sections efficaces σ(e+e– ➛ hadrons) = Σquarks Q2 e4 |M|2
➡ R = Σquarks Q2
⇒ R = constante = 2/3 ne dépendant pas de l'élément de matrice mal connu M
ou R = 2 en multipliant par 3 pour la couleur ➡manière indépendante de vérifier l'idée de couleur des quarks
Que disaient les expériences en juillet 1974 ?
Une conférence internationale se tenait cet été là, et la situation était très confuse

mais R ne semblait ni proche de 2/3 ni proche de 2, mais variait chaotiquement d'une expérience à une autre
SLAC - novembre 1974

ou en zoomant sur la région autour de 3.1 GeV

Que s'était-il passé?
La découverte du ψ
Burton Richter (à SLAC)
bizarreries des sections efficaces e+e– autour de 2x1.5 GeV à Frascati (AdA puis Adone)
collisionneur e+e– SPEAR au SLAC (1972) : 3+3 GeV
mesure minutieuse de la section efficace par très petits pas en énergie
➡ résonances très étroites : ψ à 3.097 puis ψ‘ à 3.686 GeV
La découverte du J/ψ
Samuel Ting (ce qui s'écrit 丁 en chinois)
à Brookhaven, découverte simultanée d’une particule de 3.1 GeV par mesure de la masse invariante e+e–

Interprétation : méson cc
Puis ensuite autres mésons cc (ψ‘, ψ‘’… = charmonium)
mésons D (uc, dc) et Ds (sc)
baryons charmés Λc …
R = σ(e+e–➛hadrons)/σ(e+e–➛µ+µ–) = Σquarks Q2

Après le muon, encore un lepton non prévu !
Toujours à SLAC-SPEAR, Martin Perl et ses collaborateurs avaient en 1974 d’autres événements bizarres :
«nous avons découvert 64 événements de la forme
e+ + e– → e± + μ∓ + au moins deux particules non détectées
pour lesquels nous n’avons pas d’explication conventionnelle»

➡ suggestion : e+ + e− → τ+ + τ− → e± + μ∓ + 4ν
où le τest un (troisième) lepton, de masse 1776.82 ± 0.16 MeV
le symboleτ[et ensuite le nom tau ou tauon] vient du mot τρίτον (le troisième)
Controverse initiale car le seuil de production est très proche de celui des mésons charmés D à 1865 MeV
Controverse résolue par la mesure d’un spin ½ pour le τ⇒ ce n’est pas un méson
Nouveaux fermions
Mais un lepton τanalogue au muon et à l’électron ➡ neutrino ντ associé ?
Et probablement un nouveau doublet de quarks pour compléter la famille (et corriger l’anomalie d’Adler-Bell-Jackiw)
Le quark bottom
1977 : découverte du ϒ (upsilon)
méson bb de masse 9.46 GeV
puis autres mésons bb
puis autres mésons ub, db, sb, cb,
et baryons contenant un (ou plusieurs) quark b
Le quark top
Fermilab/Tevatron/CDF
Paire top-antitop ➡ mtop = 175 GeV

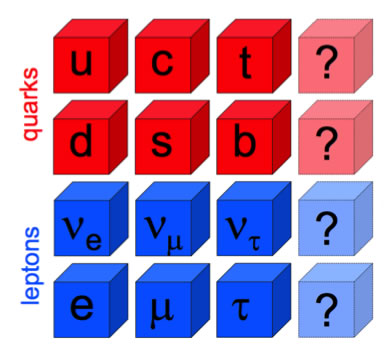
Les fermions maintenant au complet?
3 paires de quarks u et d, c et s, t et b
et 3 paires de leptons e et νe, µ et νµ, τ et ντ

Les "jets"
Montée en énergie ⇒ le nombre total de particules produites dans une collision augmente

Nombre de particules secondaires dans une collision
Modèle des quarks
- production initiale de 2 quarks
- qui « s’habillent »
- ➡ 2 jets de particules
- ± dos à dos

QCD
- production additionnelle de gluons
- qui « s’habillent »
- ➡ 3 jets coplanaires de particules
observés en 1979 par Jade et Tasso
Production de 2 jets dans une collision proton-proton, vue par l'expérience Atlas au LHC

L'observation des bosons W et Z
Collisions proton-antiproton
Idée de base : collisions à une énergie suffisante (dans le centre de masse) pour matérialiser des W et des Z
1976 : seulement possible avec les protons de 400 GeV du SPS (Cern) ou du Tevatron (Fermilab)
Modification du SPS avec 2 faisceaux de 270 GeV en sens inverse

Refroidissement stochastique des antiprotons
Difficulté : les antiprotons (produits par collision de protons) ont une grande dispersion de vitesse (⬄ ils sont « chauds »)
☛ faible taux de collision antiproton-proton
☛ énergie de la collision imprécise
Simon van der Meer

remarqua que π > 2 ☛
idée pour corriger la dispersion (⬄ « refroidir » les antiprotons) en accélérant les lents et freinant les rapides
☛ détecter leur vitesse
☛ transmettre l’information via le diamètre pendant que les antiprotons font le tour
puis répéter l’opération avant d’extraire les antiprotons (à 3.5 GeV)
et de les injecter dans le SppS pour les accélérer à 270 GeV

UA-1
Deux détecteurs furent installés autour du tube de l’accélérateur
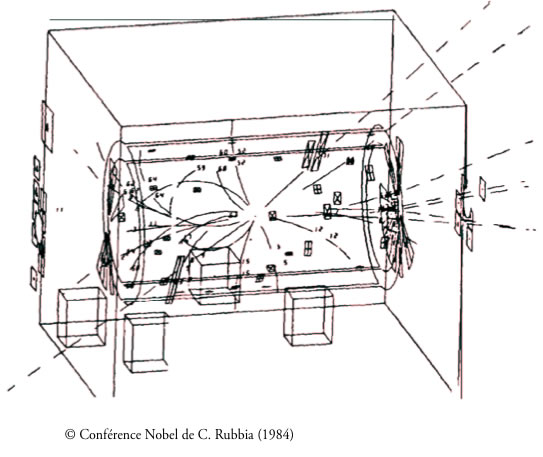
UA-1 [Rubbia]
détecteur central cylindrique (6 m de long, 2 m de diamètre) : chambres à fils entouré de calorimètres hadroniques et de détecteurs de muons

Détecteur central d'UA-1

UA-2 [Darriulat]
plus spécialisé (pas de mesure de la charge, pas de détection de muons)
mais plus précis
☛ permit de « contrôler » UA-1
1983 découverte de W ➛ eν ➡ mW = 80.4 GeV
puis découverte de Z0 ➛ e+e– ➡ mZ = 91.2 GeV
Chambre multifils proportionnelle
 Georges Charpak (1968)
Georges Charpak (1968)

Le W

W➛eν dans UA-1
Le Z
Sélection des événements où un électron et un positron ont de très grandes impulsions transversales
Élimination du bruit de fond des jets hadroniques

Z0➛e+e– dans UA-1
LEP
Les accélérateurs du CERN (en 2013)

Le LEP
Accélérateur électron-positron
accélération initiale par le SPS puis injection dans l’anneau principal
énergie initiale (1989) : 2x45 GeV ➡ production du Z0

puis montée à 170 GeV en 1995 ➡ production d’une paire W+ W–

puis d’une paire de Z0

e+e– ➛ Z0Z0 ➛ 2 jets de hadrons et une paire µ+µ– (expérience Delphi)
finalement ↗ 209 GeV fin 2000 (➡ Boson de Higgs à 115 GeV ?)
Détecteurs
Quatre détecteurs, et quatre expériences complémentaires
- Aleph
- Delphi
- L3
- Opal
Objectifs
➡ «modèle standard» à l’épreuve des mesures précises
➡ masses et largeurs des W et Z
➡ QCD perturbatif (précision qq %)
Masse et largeur du Z
Largeur ⬄ durée de vie
⬄ nombre de canaux de désintégration
⬄ nombre de champs couplés au Z0
⬄ nombre de neutrinos
Nν = 2.994 ± 0.012

➡ 3 familles de leptons
➡ 3 familles de quarks
LHC
Le LHC
Réflexions sur un supercollisionneur > Tevatron de Fermilab dès 1984
CERN
décision de réemployer le tunnel de 27 km du LEP pour un collisionneur proton-proton avec une énergie de 2x7 TeV (2x4 en 2013)
☛ mise en route en 2008 (coût 3 G€)

USA
construction d’un Superconducting SuperCollider [SSC ou Desertron] de 87 km (énergie de 2x20 TeV)
arrêtée en 1993 après que 2 G$ aient été dépensés (12 G$ prévus)
Objectifs
Objectif premier : le boson de Higgs ou les bosons de Higgs

Autres objectifs
- plasma quark-gluon
- recherche de la supersymétrie
- recherche de la matière noire
Plusieurs expériences ± simultanées
- Atlas : higgs, susy… [3000 physiciens, 174 laboratoires de 38 pays]
- CMS : higgs, susy… [2500 physiciens et 1800 ingénieurs, 179 laboratoires de 41 pays]
- LHCb : beauté et asymétrie matière-antimatière
- ALICE : ions lourds

Une collaboration à grande échelle: Atlas
Ce que représentent 3000 physiciens: la liste des collaborateurs de l'article annonçant la possible découverte du boson de Higgs en 2012




4° génération ?
Contraintes très fortes sur une éventuelle 4° génération de quarks et de leptons
Cosmologie : 3 particules de masse nulle (ou négligeable) lors de la nucléosynthèse
LEP : largeur du Z0 ➡ nombre de neutrinos = 2.994 ± 0.012
Mais cela n'empêche pas le LHC d'en chercher les traces éventuelles
Supersymétrie ?
À chaque fermion son boson
À chaque boson son fermion

Aucune s-particule observée ➡ très lourdes ?
➡ le LHC en cherche les traces
La matière noire serait-elle une s-particule ? ➡ neutralino (=photino-zino-higgsino)
L'accélérateur
Deux faisceaux de protons de 3.5 TeV chacun, en sens inverse ➡ 7 GeV (en 2012)

Faisceau de protons au LHC (KEK est un laboratoire japonais, Fermilab un laboratoire américain)
se croisant en 4 points

1400 paquets de 1011 protons chacun, dans chaque sens (15 millions de croisements de paquets par seconde)
Un paquet : quelques cm de long, quelques mm de diamètre, réduits à quelques microns aux points d’intersection
➡ 109 interactions/s ➡ analyse toutes les 25 ns (7.5 m à la vitesse de la lumière) de ~ 25 collisions superposées produisant chacune ~ 50 traces ⤷

Un détecteur : CMS
Diamètre : 15 m
Longueur : 21.6 m
Poids : 12 500 tonnes

Du centre à la périphérie
- détecteur de vertex
- trajectographe en silicium (suit les particules chargées)
- calorimètre électromagnétique (absorbe électrons et photons)
- calorimètre hadronique (absorbe les jets de hadrons)
- chambres à muons (visibles dans le trajectographe mais pas dans les calorimètres)
le tout dans un champ magnétique solénoïdal de 4 T

Identification des particules

Le boson de Higgs
Simulation de Higgs dans CMS au LHC, selon le processus H ➛ Z0 Z0 ➛ e+ + e– + 2 jets de hadrons
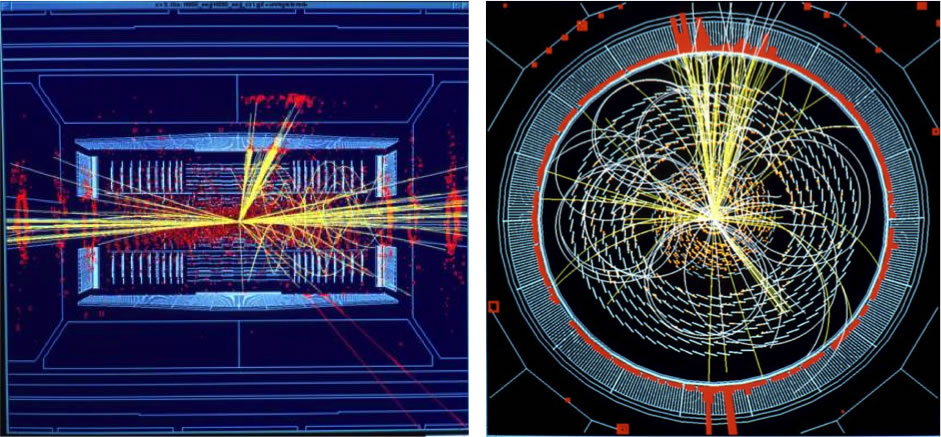
LHC-ATLAS : événement 2 électrons + 2 muons pouvant résulter d’une désintégration d'un boson de Higgs

Masse invariante de 4 leptons (expérience CMS)

Masse invariante de 4 leptons [ATLAS]

Tout est question de statistique
Une autre possibilité : H0 ➛ 2γ
Le boson de Higgs est couplé à une particule proportionnellement à la masse de celle-ci
➡ couplage de préférence au quark top, ou aux W et Z

Masse invariante des 2γ ⇒ masse du higgs
Résultat

Le modèle standard
Champs de matière
Tous de spin ½ et de masse nulle
Les fermions : quarks et leptons
 Première génération de quarks et leptons : toute la matière autour de nous
Première génération de quarks et leptons : toute la matière autour de nous
Pourquoi deux autres générations? Pourquoi trois familles rigoureusement identiques (à la masse près)?
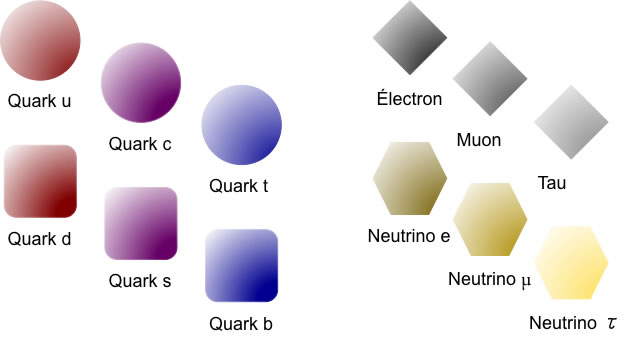
Connectés par certaines symétries (⬄ redondance de la description)
Locales
U(1)
SU(2)
SU(3)
Globales
SU(6)
PCT
Lorentz-Poincaré
Symétries locales
⬄ interactions entre champs de matière
Portées par des champs (de jauge)
de spin 1
et de masse nulle
Trois symétries de jauge (symétries internes locales)
Interaction électromagnétique ☜ invariance de phase U(1) ☞ photon
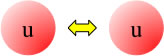
Interaction faible ☜ invariance de phase SU(2) ☞ W+, W– et Z0

Interaction forte ☜ invariance de phase SU(3) ☞ gluons

Masse
Quanta massifs ➡ brisure spontanée de symétrie
➡ champs additionnels de spin 0 (➡ les bosons de Higgs)
➡ masse pour les champs de jauge [correspondant aux symétries brisées]
➡ masse pour les champs de matière [couplés aux champs de Higgs]
➡ au moins un boson de Higgs doit être encore présent après brisure
Interaction forte
Questions de statistique
Modèle des quarks (Gell-Mann, Zweig 1964)
➡ quelle interaction associe 3 quarks en baryon, ou quark-antiquark en méson ?
➡ pourquoi n’y a-t-il pas de combinaisons qq, qqq, qqq, etc. ?
➡ pourquoi le principe de Pauli ne s’applique-t-il apparemment pas à certains baryons ?
- Ω– : 3 quarks s de spins ↑↑↑ (Struminsky 1965)
- Δ++ : 3 quarks u de spins ↑↑↑
- Δ– : 3 quarks d de spins ↑↑↑
Solution de Greenberg (1965) : parastatistiques
les quarks suivent une parastatistique différente de Fermi-Dirac
Solution de Han et Nambu (1965) : couleur
les quarks possèdent un nombre quantique additionnel, la « couleur »
➡ symétrie SU(3)
➡ mais globale ou locale ?
3 couleurs nécessaires pour différencier les 3 quarks u du Δ++ [et les 3 d du Δ– et les 3 s du Ω–]
mais pas 4 couleurs, sinon états qqqq possibles, mais non observés
➡ 3 quarks de 3 couleurs différentes dans un baryon ➡ couleur totale nulle
➡ un quark et un antiquark de couleurs opposées dans un méson ➡ couleur totale nulle
➡ toute autre combinaison est colorée, et ne peut exister librement [à démontrer ! ]
Couleur n’est pas saveur !
Attention à la confusion entre le SU(3) de la couleur et le SU(3) originel de Gell-Mann et Zweig, la saveur!
Chromodynamique quantique (QCD) : théorie de jauge basée sur un groupe de symétrie SU(3)
Saveur
Le modèle de Gell-Mann et Zweig avec 3 quarks u, d et s utilise aussi le groupe SU(3)
Mais c’est une symétrie globale
u ↔ d ↔ s
(d’ailleurs approximative parce que le quark s est plus lourd que les 2 autres)
Prédiction puis observation des quarks c b et t ➡ groupe SU(6) de symétrie globale approximative
u ↔ d ↔ s ↔ c ↔ b ↔ t
➡ 6 saveurs de quarks
Couleur
Symétrie SU(3) locale exacte
➡ 3 possibilités, 3 couleurs de quarks
rouge R – vert V – bleu B ( ex. quark R antiquark B )
➡ 8 bosons de jauge de masse nulle gluons « colorés » par ex. RV
➡ interaction quark-quark-gluon
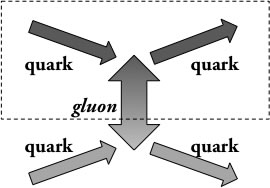
➡ interaction gluon-gluon-gluon
➡ hadrons incolores ⇔ q.q.q ou q.qbar
SU(3) : chromodynamique quantique
Groupe SU(n)
➡ représentation fondamentale à n éléments ➡ 3 couleurs possibles pour un quark
➡ représentation adjointe à n2 – 1 éléments ➡ 8 gluons pour relier deux quarks
![]()
➡ LQCD = …+ ψ*γµAµψ +…
➡ gluon = couleur + anticouleur
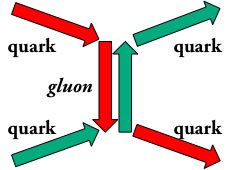
Le proton (vision d’artiste !)

Renormalisation de la constante de couplage
αS diminue quand l’énergie augmente
Corrections radiatives fermions ➡ α augmente

bosons ➡ α diminue

Résultat:

Liberté asymptotique
Interaction forte ➘ à haute énergie = «liberté asymptotique» [Gross, Politzer et Wilczek 1973]
➡ QCD perturbatif testé par les mesures précises du LEP
➡ inversement, couplage ➚ à basse énergie ⬄ grande distance ➡ confinement de la couleur ? Prix Clay de 1 M$ à celui qui le démontrera…
Mais on a souvent besoin de connaître le comportement à basse énergie
- ex : calcul des masses des hadrons
- ex : désintégration méson D ➛ Keν

➡ QCD sur réseau

Groupe de renormalisation
Idée ancienne (Pythagore, Euclide, Galilée) d’invariance par changement d’échelle
Groupe des transformations d’échelle (Stückelberg et Peterman1953, Gell-Mann et Low 1954, Bogoliubov et Shirkov 1955)
le point µ en énergie où sont mesurées les masses et constantes de couplage est arbitraire
➡ règle pour passer d’une valeur µ à une valeur µ’
➡ équations ∂g/∂µ = β(g)
avec une fonction β(g) dépendant de la théorie
➡ g(µ)
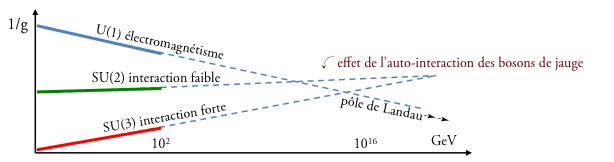
Groupe de renormalisation et évolution avec l'énergie des constantes de couplage
Kenneth Wilson 1971
application à la matière condensée, aux transitions de phase et aux phénomènes critiques (Nobel 1982)
➡ nouveau point de vue sur le sens physique de la renormalisation

Interaction électrofaible
SU(2)LxU(1)Y
Quarks et leptons
séparation en composantes «gauches» et «droites»
ψL = ½(1 - γ5)ψ et ψR = ½(1 +γ5)ψ
composantes ψL formant des doublets de SU(2)L
composantes ψR formant des singlets de SU(2)L

⬄ seules les composantes ψL sont soumises à l’interaction faible
⬄ brisure (explicite) de la parité ψL ⟷ ψR
Symétries locales
➡ dérivées covariantes ➡ champs de jauge
W+ , W0 et W– pour SU(2)L transformant uL en dL par exemple

B0 pour U(1)Y
Deux groupes de jauge différents ➡ deux constantes de couplage indépendantes
- g2 pour SU(2)L
- g1 pour U(1)Y
Brisure spontanée de SU(2)LxU(1)Y
Mécanisme de Higgs, Brout-Englert et Guralnik-Hagen-Kibble
➡ requiert un doublet [complexe] de SU(2)L
⬄ 4 champs réels
et un potentiel « sombrero »

➡ le minimum du potentiel
- est un choix de direction dans SU(2)L ➡ brisure de SU(2)L
- est un choix de phase U(1)Y ➡ brisure de U(1)Y
- ➡ on ne peut pas briser SU(2)L sans briser aussi U(1)Y
mais il reste une invariance de phase résiduelle ➡ il reste une symétrie U(1)em non brisée
Angle de Weinberg
➡ une des combinaisons de W0 et B0 demeure de masse nulle
➡ photon γ
l’autre acquiert une masse
➡ Z0
➡ angle θW donné par sinθW = g1/[g12+g22] ½

➡ MZ = MW/cosθW ➡ θW ~ 30°
3 champs donnent leurs masses aux W+, W– et Z0 ➡ il en reste un !
La masse des fermions
Terme de masse « normal » d’un fermion ψ
☛ mψ*ψ
ψ = ψL + ψR ➡ m [ψL*ψR + ψR*ψL ] ➡ viole SU(2)L
➡ les fermions (quarks et leptons) devraient avoir une masse nulle
Solution
coupler les fermions aux champs de Higgs φ
car un terme du genre λφψL*ψR [couplage de Yukawa] ne viole pas SU(2)L
quand la symétrie est (spontanément) brisée φ ➛ φ0 + φ’
➡ terme de masse effectif λφ0ψL*ψR
➡ masse mψ = λφ0
⬄ la masse est d’autant plus grande que le couplage λ est grand
⬄ le champ de Higgs est d’autant plus fortement couplé à un fermion que celui-ci est lourd
➡ chercher le boson de Higgs dans les désintégrations du quark top ou des W et Z
Mais les couplages de Yukawa des différents fermions sont autant de paramètres libres
Découverte du boson de Higgs au LHC

La matrice de Cabibbo-Kobayashi-Maskawa
La base des états propres de masse des quarks diffère de la base des états propres de l’interaction faible
➡ matrice de rotation 3x3 (dans l’espace des familles)
K = s+d D = c+d Bd = b+d Bs = b+s Bc = b+c
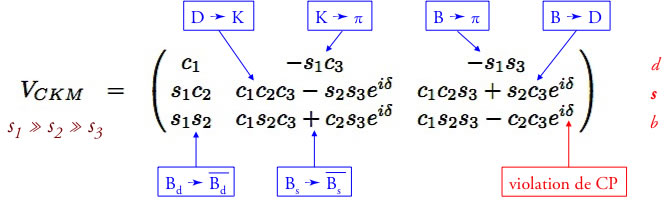
Même chose pour les leptons ➡ matrice de Pontecorvo-Maki–Nakagawa–Sakata
➡ oscillations de neutrinos : ce sont les états propres de masse qui se propagent et les états propres d'interaction qui… interagissent.
Le lagrangien du modèle standard
En recollant tous les morceaux:
