Alain Bouquet - Théorie quantique - Formalisme

En fait, ce n'est pas toujours le cas! L'énergie n'est pas toujours quantifiée (ni les états quantiques discrets): par exemple, des électrons libres ont une énergie continue. L'aspect probabiliste est présent, mais il n'est pas nécessairement central, il peut être vu comme un effet collatéral dans la théorie quantique. La différence majeure entre physique classique et quantique est plutôt que:

l'espace des états n'a aucune structure en physique classique ;
l'espace des états est un espace vectoriel (complexe en plus) en physique quantique.

La notion d'état d'un système

En physique "classique"

la physique est avant tout l'étude du mouvement, et plus précisément l'étude des déplacements dans l'espace.

Succession de points de vue: Aristote ➛ Philoponus ➛ Oresme ➛ Galilée ➛Newton ➛Lagrange ➛ Liouville ➛ Poisson ➛ Hamilton

Mécanique du point matériel, soumis à une force (Newton) puis progressivement placé dans un champ de force. Deux points de vue possibles:

les points sont soumis à des forces dans un espace qui est, lui, dénué de propriétés (Démocrite, Newton)
les points sont soumis aux effets du lieu (= les propriétés de l'espace) où ils se trouvent (Aristote, Faraday, Einstein)

Mécanique d'un ensemble de points matériels:

indépendants les uns des autres ➛exemple: la thermodynamique statistique des gaz
indépendants les uns des autres mais placés dans un même champ de force
interagissant les uns avec les autres

☛ définition d'un système physique

isolé
sous-ensemble d'un système plus grand (➛interactions entre les parties de ce grand système)

Etat du système

Système décrit par un ensemble de variables, dont les valeurs définissent un des états possibles du système:

point matériel: position et vitesse. On peut préciser des paramètres comme la masse ou la charge éventuelle (mais celles-ci ne changent normalement pas)
thermodynamique: pression, volume, température, entropie, énergie (quantités qui ne sont pas indépendantes).

La liste des états possibles peut être

finie (et donc numérotable pas une suite de nombres entiers)
infinie dénombrable
infinie continue

Dans une vision du monde où la matière peut être décomposée en éléments irréductibles, comme les atomes au sens de Démocrite, tout système physique est réductible à la donnée de la liste des ces éléments avec pour chacun d'eux sa position q et sa vitesse v=∂q/∂t, ou de manière équivalente son impulsion p=mv. On peut effectuer, au moins formellement, la même démarche pour une matière continue en la découpant en petits éléments (dénombrables), dont la taille tend vers zéro à la fin.

Espace de phase

Pour un système réduit à une particule unique, chaque état est défini par la donnée du couple (v,q) ou de façon équivalente (p,q). Pour un système à une dimension, le couple (p,q) définit un point dans un espace à deux dimensions, l'espace de phase. Un point matériel qui évolue dans un espace à trois dimensions nécessite trois coordonnées (x, y et z en coordonnées cartésiennes, r, θet φ en coordonnées polaires),que l'on peut noter q et son impulsion a également trois composantes, notées p. L'espace de phase (p, q) a donc six dimensions. L'espace de phase d'un système de N points matériels aura 6N dimensions.

L'ide de représenter un système physique par un point unique dans un espace avec un grand nombre de dimensions ne s'est fait jour que lentement (cf. D.N. Nolte, Physics Today, avril 2010). D'une part imaginer un espace qui ait plus de trois dimensions n'avait rien de naturel, bien que les mathématiciens aux 17° et 18° siècles aient manipulé sans souci un grand nombre de variables simultanées, et n'est que peu à peu devenu "pensable" avec les travaux de Cayley (1843), Grassmann (1844), Plücker ou Sylvester, puis surtout avec Riemann (1854 puis 1868), avant de se généraliser avec Felix Klein et Camille Jordan.

Boltzmann utilisa implicitement la notion d'espace de phase (mais pas le terme) dès sa thèse de 1866 sur la théorie cinétique des gaz et son cours de dynamique (Vorlesungen über Dynamik 1866), puis dans ses articles fondamentaux de 1871. Dans l'un de ces articles, il compare la trajectoire engendrée par le mouvement à une dimension d'une particule et sa vitesse (ou son impulsion) avec la trajectoire d'une particule dans un espace à deux dimensions, et il note une analogie avec une courbe de Lissajous (sans nommer Lissajous d'ailleurs). C'est l'origine du mote "phase": une courbe de Lissajous est la trajectoire d'un point de coordonnées {x(t), y(t)} quand les deux fonctions x(t) et y(t) sont des fonctions périodiques. Si les périodes sont dans un rapport rationnel, la courbe est fermée (1° figure ci-dessous pour l'exemple 3:2) et elle se modifié selon la phase relative des deux fonctions (2° courbe ci-dessous):

Lissajous

Courbes de Lissajous (Wikipedia)

Dans le cas de smouvements complexes des atomes ou des molécules d'un gaz, Boltzmann distinguait le type du mouvement (Bewegungsart), par exemple un mouvement de translation ou de rotation, de la phase du mouvement (Bewegunsphase) correspondant au changement de position ou d'impulsion. Maxwell reprit en 1879 le terme de phase introduit par Boltzmann pour désigner le couple {position, impulsion} décrivant l'état d'un système à une particule, et plus généralement les N-uples {qi, pi} pour l'état d'un système de N particules. Mais ni Boltzmann ni Maxwell ne concevèrent un espace de phase. Boltzmann lui-même ne réemploya pas le terme de phase avant son traité de 1896 sur la théorie cinétique des gaz (Vorlesungen über Gastheorie).

Entretemps, Henri Poincaré avait étudié le comportement de systèmes dynamiques, et en particulier la manière dont les trajectoires approchaient de solutions quasi-stables (points fixes ou cycles limites). En appliquant cette approche au problème de la stabilité du système solaire, sous la forme a priori plus simple du problème des trois corps, Poincaré découvrit à la fin de l'année 1889 que de très faibles changements des positions initiales pouvaient conduire à des très grand changements des positions finales, ce qui est point de départ des travaux contemporains sur le "chaos déterministe". À cette occasion, Poincaré développa une approche géométrique dans laquelle il étudiait le mouvement d'un point dans un espace à 6N dimensions, l'espace de phase (mais sans lui donner ce nom).

Poincaré

Le terme d'espace de phase (Phasenraum) apparut finalement, sous la plume de Paul et Tatiana Ehrenfest en 1911, dans une revue de l'oeuvre de Boltzmann écrite pour la grande Encyclopédie des sciences mathématiques dont Felix Klein était le moteur. l'usage s'en généralisa ensuite progressivement.

Exemple d'un oscillateur harmonique

Masse m soumise à une force de rappel F = -kq proportionnelle au déplacement q

⇒ équation du mouvement de Newton F = mγ où l'accélération γ = d²q/dt²
⇒ d²q/dt² +k/m q = 0
⇒ q(t) = q_max cos[ωt] où ω²=k/m et q_max le déplacement maximal
⇒ p(t) = m dq/dt = p_max sin[ωt]

☛ au cours du temps, le point de coordonnées (p,q) décrit un cercle dans l'espace de phase.

Pendule simple

Un pendule simple est une masse m suspendue à un fil ou une tige rigide de longueur l dans le champ de pesanteur g (supposé uniforme). Sa position est repérée par l'angle θ du fil avec la verticale.

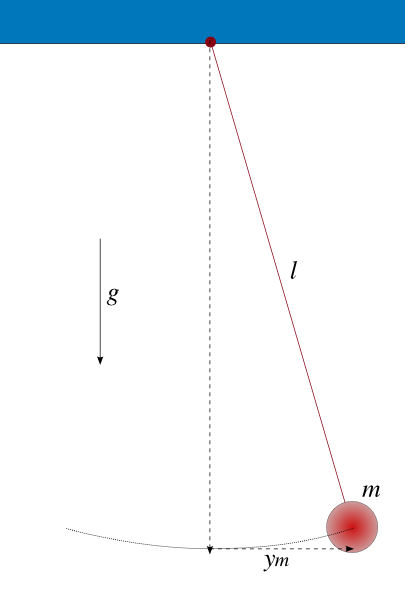
Pendule simple

En notant θ'=dθ/dt et θ"=d2θ/dt2 les dérivées première et seconde d el'angle θ par rapport au temps t, l'équation du mouvement du pendule est

θ" + g/l sin θ = 0

Pour de petits angles θ, sinθ~θ et l'équation devient une équation harmonique de pulsation ω=√(g/l), dont la solution est

θ(t) = θ(0) cos ωt

La période T = 2π/ω = 2π√(l/g) ne dépend pas de l'amplitude initiale θ(0) mais seulement d ela longueur l du pendule: c'est l'isochronisme des petites oscillations découverte par Galilée. Pour des oscillations de plus grande ampleur, sinθ≠θ et la période dépend de l'amplitude initiale. Enfin, pour une énergie totale (cinétique+potentielle) supérieure à 2mgl, le pendule effectue des rotations autour du point de suspension. Un manière parlante de différencier les deux types de mouvement possibles est d'introduire le puits de potentiel du pendule. L'énergie potentielle est E_p = mgl(1-cosθ) et, tracée en fonction de l'angle θ, a la forme d'une cuvette (ou d'un puits) de profondeur 2mgl. Si l'énergie totale est inférieure à 2mgl, il existe un angle maximal θ₀ où la vitesse θ' (et donc l'énergie cinétique) s'annule, et le pendule oscille entre θ₀ et –θ₀ . Si l'énergie totale est supérieure à 2mgl, la vitesse ne peut pas s'annuler et le pendule tourne en cercle autour du point de suspension.

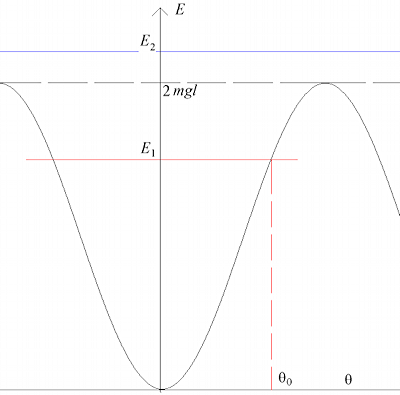
Puits de potentiel du pendule

D'où les deux zones de l'espace de phase d'un pendule:

Espace de phase d'un pendule

Espace de phase pour un pendule: l'angle θ est porté sur la coordonnée horizontale, la vitesse angulaire θ' sur la coordonnée verticale, les trajectoires en noir sont les oscillations du pendule autour de sa position d'équilibre au repos (point S), les trajectoires en rouge sont les rotations autour du point de suspension du pendule (Wikipedia).

Évolution au cours du temps

L'évolution au cours du temps d'un système physique, c'est passer d'un état du système à un autre état du système. Ceci est régi par des lois du mouvement qui, en physique classique ont en général la forme d'équations différentielles. Ce n'est pas une exigence mathématique et il est possible d'imaginer des systèmes tels que le passage de l'état i à l'état j soit donné par des lois arbitraires. Par exemple le "jeu de la vie" imaginé par Conway qui conduit à des évolutions très complexes, et plus généralement toute la théorie des automates, ainsi que les machines de Turing.

Ces systèmes peuvent être déterministes (la transition i➛j de l'état i à l'état j est déterminée sans ambiguïté) ou aléatoires (l'état i peut conduire aux états j, k, l… suivant certaines lois de probabilité). Ils peuvent par ailleurs être réversibles (la succession de transitions i➛j➛k donne par renversement du temps la succession k➛j➛i) ou non. L'irréversibilité est le cas général (il suffit que l'on ait comme transitions possibles i➛j➛k et l➛j➛k pour que k➛j➛?).

Les lois d'évolution des systèmes étudiés en physique classique représentent donc un cas très particulier de toutes les lois imaginables: elles sont à la fois déterministes et réversibles.

Le second principe de la thermodynamique (l'entropie d'un système isolé ne peut que croître au cours du temps) semble une exception, et 150 ans d'efforts n'ont pas abouti à l'intégrer de façon complètement satisfaisante dans le cadre déterministe et réversible de la physique.

Newton-Lagrange-Hamilton

Poisson

Transformation de Fourier

Ensemble des états

L'ensemble de tous les états possibles est un ensemble au sens de la théorie mathématique des ensembles, dont les états sont les éléments.

Ces éléments sont disjoints.

Ceci signifie que les états possibles sont distincts les uns des autres. Une pièce de monnaie est un système avec deux états possibles, que l'on peut noter "pile" et "face", 0 et 1, "blanc" et "noir", "+" et "–" ou tout autre notation binaire qui convient. Un pièce est nécessairement soit dans l'état "pile", soit dans l'état "face", et il n'existe aucune autre possibilité. Un éventuel observateur peut ignorer dans quel état se trouve la pièce, mais la pièce, elle, ne peut pas se trouver simultanément dans l'état "pile" ET dans l'état "face": il n'existe pas d'état "quelque part entre les deux".

Cela est vrai aussi des états continus: l'oscillateur harmonique se trouve à un instant donné soit dans l'état (p,q), soit dans un état différent (p',q'), mais il ne peut pas se trouver en même temps dans l'un ET dans l'autre. Sauf quand il s'agit d'ondes.

Il est possible de définir des sous-ensembles d'états, et de leur appliquer les opérations classiques d'union et d'intersection. Il est également possible d'énoncer de spropositions portant sur ces sous-sensembles et de leur appliquer la logique classique des propositions (si A est vrai et B est vrai, alors A et B est vrai; si A est vrai et B est faux, alors A ou B est vrai…).

En physique quantique

Les notions de système physique, de sous-système, de système isolé perdurent en physique quantique, de même que la notion d'état d'un système. Mais par contre la disjonction des états disparaît en physique quantique.

L'ensemble des états possibles d'un système quantique possède une structure d'espace vectoriel.

Ceci signifie que la notion de somme de deux états a un sens, et que cette somme est aussi un état possible du même système. Les espaces vectoriels sont omniprésents en physique: l'espace euclidien a une structure d'espace vectoriel, de même que les fonctions généralement utilisées. Mais ce n'était pas le cas pour l'ensemble des états d'un système. Sauf quand il s'agit d'ondes.

C'est la structure d'espace vectoriel qui est à l'origine des "paradoxes" de la physique quantique parce qu'elle permet à un état d'être la somme de deux autres états. Ce n'est PAS un état plus ou moins intermédiaire entre ces deux états mais bien un état qui est en même temps l'un ET l'autre.

Espaces vectoriels

Un espace vectoriel E est un ensemble d'éléments (les "vecteurs" de E) doté de deux lois de composition linéaires:

addition : si A est un vecteur et B est un vecteur, alors A+B est un vecteur de E (l'espace E a une structure de groupe abélien pour l'addition);
multiplication scalaire: si A est un vecteur et α un nombre ("scalaire"), alors αA est un vecteur du même espace.

Le nombre α peut être un nombre réel (α∈ℝ), complexe (α∈ℂ) ou plus généralement un élément d'un corps K. En mécanique quantique, ce sera un nombre complexe.

La structure de groupe abélien pour l'addition signifie que

il existe un vecteur nul 0, tel que ajouté à tout vecteur A il redonne le vecteur A: A+0=A
tout vecteur A possède un opposé, noté -A tel que leur somme soit le vecteur nul: A+(-A)=0
l'addition est distributive: A+(B+C) = (A+B)+C = A+B+C
l'addition est commutative (ce qui rend le groupe abélien): A+B=B+A

La multiplication scalaire est:

distributive par rapport à l'addition sur l'espace E: α(A+B) = αA + αB
distributive par rapport à l'addition sur le corps K: (α+β)A = αA + βA
associative par rapport à la multiplication sur le corps K: (αβ)A = α(βA)

Par conséquent, toute combinaison linéaire de vecteurs αA+βB+γC+… de E est encore un vecteur de E.

Bases d'un espace vectoriel

Si toute combinaison linéaire de vecteurs αA+βB+γC+… est encore un vecteur, inversement tout vecteur peut s'écrire comme combinaison linéaire d'autres vecteurs. On peut donc naturellement se demander s'il existe un jeu de vecteurs à partir desquels on peut obtenir n'importe quel vecteur de l'espace vectoriel E. Cela existe toujours (on parle de famille génératrice), et il y en même une infinité puisque n'importe quelle combinaison linéaire des vecteurs de cette famille permet d'en construire d'autres. parmi tous les vecteurs d'une famille génératrice, on peut choisir ceux qui sont linéairement indépendants, c'est-à-dire ceux dont toute combinaison linéaire nulle a nécessairement tous ses coefficients nuls.

Un tel ensemble de vecteurs indépendants à partir desquels on peut obtenir n'importe quel vecteur par la combinaison linéaire appropriée s'appelle une base de l'espace vectoriel E. En fait il existe une infinité de bases, obtenues par combinaison linéaire les unes des autres, mais le nombre de vecteurs de base demeure toujours le même: c'est une caractéristique de l'espace vectoriel, que l'on appelle la dimension de l'espace. Cette dimension peut être infinie (dénombrable ou non).

Exemple: espace euclidien à deux dimensions.

Exemple: qubit à deux états

Notation de Dirac

Les éléments d'un espace vectoriel sont appelés des "kets", et ils sont notés de la façon suivante: |Ψ>. Cette notation, due à Paul Dirac, a l'avantage de bien séparer, visuellement, un vecteur (=élément de l'espace vectoriel E) noté |Ψ> d'un scalaire (=élément du corps K) qui pourrait lui aussi s'appeler Ψ. Mais l'intérêt (et la puissance) de la notation de Dirac apparaîtra après l'introduction de l'espace dual E* et surtout des opérateurs linéaires agissant sur l'espace vectoriel E.

Si {|i>} est une base de l'espace vectoriel E, tout vecteur |Ψ> s'exprime comme une combinaison linéaire unique des vecteurs de la base.

|Ψ> = Σ_i α_i |i>

Les coefficients α_i sont appelés les composantes du vecteur dans la base |i>. Pour noter un vecteur, on utilise plus traditionnellement la notation (α₁, α₂, …, α_n) souvent écrite sous la forme d'une colonne de nombres (un tableau à une dimension).

Dual E* d’un espace vectoriel E (espace adjoint)

Le dual E* d'un espace vectoriel E est l'espace des formes linéaires, une forme linéaire sur un espace vectoriel E étant une application linéaire de l'espace E sur le corps K, autrement dit une fonction Φ qui associe à tout vecteur Ψ un nombre (complexe) Φ(Ψ).

Dans la notation de Dirac, les éléments du dual sont appelés "bras" et notés <Φ|.

Il existe une bijection entre les éléments d'un espace vectoriel et les éléments de son dual:

<i| ⇌ |i>
<i| + <j| ⇌ |i> ± |j>
α* <i| ⇌ α |i>

Le dual d'un espace vectoriel est aussi un espace vectoriel, et de même dimension ! Il est isomorphe à E, d'où la possibilité d'identifier chaque élément du dual à un élément précis de l'espace vectoriel, en leur donnant le même nom par exemple.

Base duale

<Ψ| = Σ_j α_j^* <j| (avec le complexe conjugué quand le corps K est le corps des nombres complexes)

Pour noter un élément du dual, on utilise souvent la notation (α₁^*, α₂^*, …, α_n^*) souvent écrite sous la forme d'une ligne (un tableau à une dimension) de nombres

Produit scalaire et normes

Attention: <Ψ₁|Ψ₂> = <Ψ₂|Ψ₁>^* (complexe conjugué quand le corps K est le corps des nombres complexes).

Deux vecteurs |Ψ₁> et |Ψ₂> sont dits orthogonaux si leur produit scalaire est nul. Si {|i>} est une base de l'espace vectoriel E, on dit que c'est une base orthogonale si tous les vecteurs de base sont orthogonaux deux à deux. La norme |Ψ| d'un vecteur |Ψ> est la racine carrée de son produit scalaire avec lui-même, c'est un nombre réel positif ou nul.

|Ψ| = √(<Ψ|Ψ>)

Une base est dite orthonormée si tous les vecteurs de base sont de norme égale à 1 et qu'ils sont orthogonaux deux à deux.

Si {|i>} est une base orthonormée de l'espace vectoriel E, {<j|} est une base orthonormée de l'espace dual E* et

<j|i> = δ_ij

<Ψ|Ψ> = Σ_iΣ_j α_j^*α_i <j|i> = Σ_iΣ_j α_j^*α_i δ_ij = Σ_i α_i^*α_i = Σ_i |α_i|²

[Théorème de Pythagore]

Remarque

|Ψ> = Σ_i α_i |i> ⇔ <Ψ| = Σ_j α_j^* <j|

☛ <j|Ψ> = Σ_i α_i <j|i> = Σ_i α_i δ_ij = α_j

☛ |Ψ> = Σ_i α_i |i> = Σ_i <i|Ψ>|i> = Σ_i |i><i|Ψ> (car <i|Ψ> est un scalaire)

☛ Σ_i |i><i| = Identité

Et on voit apparaître un opérateur, un objet qui n'est pas un scalaire mais qui, appliqué à un vecteur, donne un vecteur (en termes plus mathématiques, un endomorphisme de l'espace vectoriel). L'opérateur identité, appliqué à tout vecteur, redonne le même vecteur.

|Ψ₁><Ψ₂|Ψ₃> = a|Ψ₁>

En particulier, |Ψ₁><Ψ₁| est un projecteur, un opérateur qui donne la projection d'un vecteur quelconque sur |Ψ₁>.

Cas continu

Espace de Hilbert (terme de von Neumann, qui fut l'assistant de David Hilbert en 1926),

algèbre d'opérateurs etc.

Janos von Neumann (Mathematische Grundlagen der Quanten-Mechanik, 1932)

Biographie de János von Neumann?

Opérateurs

Opérateurs linéaires sur un espace vectoriel

Un opérateur O est une application de l'espace vectoriel E sur lui même, autrement dit une application qui fait correspondre un vecteur |Ψ> à un vecteur |Φ>:

O|Ψ> = |Φ>

Opérateur

Pour |Ψ> donné, |Φ> est unique. Mais la réciproque n'est pas nécessairement vraie: le même opérateur O peut "envoyer" deux vecteurs différents sur le même vecteur de destination.

Cet opérateur O est linéaire si (pour tous les scalaires α et β et tous les vecteurs |Φ> et |Ψ>) on a

O( α|Φ> + β|Ψ> ) = α O|Φ> + β O|Ψ>

β_i^* = <i|Φ> = <i| O |Ψ> = <i| O ( Σ_j α_j |j>) = Σ_j α_j <i| O |j> =Σ_j α_j O_ij

En effet |j> est un vecteur, O|j> également, <i| une forme linéaire et donc <i| O |j> un scalaire (nombre) que l'on peut noter O_ij. L'ensemble de toutes les valeurs O_ij pour toutes les valeurs de i et de j définit l'opérateur O. Pour un espace vectoriel de dimension n, ces valeurs O_ij se rangent dans un tableau carré à n lignes et n colonnes, une matrice carrée.

Dans le vocabulaire des matrices, un vecteur est une matrice-colonne, une forme linéaire, une matrice-ligne, un opérateur une matrice carrée et la relation β_i^* = Σ_j α_j O_ij un produit matriciel.

Bien entendu, les composantes d'un vecteur comme les éléments matriciels d'un opérateur dépendent de la base choisie.

Un opérateur O peut bien sûr agir sur un bra <Φ|. On définit son action de la manière suivante:

[<Φ|O] |Ψ> = <Φ| [O |Ψ>] = <Φ| O |Ψ>

En intercalant l'opérateur Identité Σ_i |i><i|

<Φ| O |Ψ> = <Φ| Σ_i |i><i| O Σ_j |j><j| |Ψ> = Σ_i Σ_j <Φ|i><i| O |j><j|Ψ> = Σ_i Σ_j β_i^* Oij α_j

Le résultat ne dépend pas du fait que l'on somme d'abord sur i ou d'abord sur j, ce qui justifie la définition.

Opérateurs conjugués

Si on a un opérateur O tel que O|Ψ> = |Φ>, existe-t-il un opérateur O^† qui, appliqué sur le bra <Ψ| donne le bra <Φ| ? Oui, mais O^† diffère en général de O. C'est le conjugué (hermitien) de O.

Ses éléments de matrice sont simples à calculer, connaissant ceux de O.

O |i> = |k> ➛ Oij = <j| O |i> = <j|k>

➛ <i| O^† = <k|

➛ O^†_ij = <i| O^† |j> = <k|j> = <j|k>* (conjugaison complexe)

➛ O^†_ij = O_ji*

La matrice de O^† est donc la transposée de la matrice de O (i⇌j) dont les éléments sont remplacés par le conjugué complexe (transjuguée).

Il se peut que les opérateurs O et O^† soient identiques, on dit alors que l'opérateur est hermitien. En ce cas, les éléments diagonaux de la matrice sont réels et les éléments non-diagonaux sont complexes conjugués. Si O = –O^†, on dit que O est antihermitien. Les opérateurs hermitiens jouent un rôle central en physique quantique car ils correspondent aux observables (les quantités physiques que l'on peut observer et mesurer).

Opérateurs orthogonaux et unitaires

Un opérateur O est unitaire si OO^† = I (et donc également O^†O = I)

Permutations

Rotations

Vecteurs propres et valeurs propres

Vecteurs propres

Un vecteur propre |λ> d'un opérateur O donné est un vecteur tel que cet opérateur appliqué à lui redonne le vecteur de départ, à une constante près:

O |λ> = λ |λ>

où le même nom a été donné au vecteur propre |λ> et à la constante de proportionnalité λ qui est un nombre complexe. On le fait souvent, quand il n'y a pas de risque d'ambigüité, mais cela n'a rien d'obligatoire. Cette constante de proportionnalité s'appelle la valeur propre de l'opérateur O relative au vecteur propre |λ>. Si |λ> est un vecteur propre de l'opérateur O, le vecteur α|λ> (où α est un nombre complexe quelconque) est aussi un vecteur propre de O, avec la valeur propre αλ.

Un opérateur donné peut avoir (et c'est en général le cas) plusieurs vecteurs propres différents, ou ne pas avoir de vecteur propre du tout. Des vecteurs propres différents peuvent correspondre à une même valeur propre, on dit alors qu'ils sont dégénérés.

Spectre des valeurs propres

Tout opérateur O tel que OO^† = O^†O (on dit que l'opérateur est normal) est diagonalisable: il existe une base (orthonormée) de l'espace vectoriel formé par les vecteurs propres. L'ensemble des valeurs propres correspondantes (le spectre) est un ensemble de nombres réels si O est hermitien, imaginaires purs si O est antihermitien, et complexes de module 1 si O est unitaire.

Il est immédiat de démontrer que les valeurs propres d'un opérateur hermitien sont toutes réelles:

De façon générale: O |λ> = λ |λ> ⇒ <λ|O^† = λ* <λ|

⇒ <λ| O |λ> = λ <λ|λ> d'une part, et <λ| O^† |λ> = λ* <λ|λ> d'autre part

Mais si O est hermitien, O = O^† ⇒ λ = λ* ⇒ λ est réel

C'est l'origine du rôle essentiel joué en mécanique quantique par les opérateurs hermitiens: leurs valeurs propres sont des nombres réels, pouvant correspondre à des résultats physiques.

Il est également immédiat de montrer que des valeurs propres différentes d'un opérateur hermitien correspondent à des vecteurs propres orthogonaux. Si on a O |λ> = λ |λ> et O |μ> = μ |μ> avec λ≠μ, alors:

<μ| O |λ> = λ <μ|λ>

<μ| O^† |λ> = <μ| O |λ> = μ <μ|λ>

⇒ [λ - μ ] <μ|λ> = 0 ⇒ <μ|λ> = 0

Discret = quantifié

Continu

Amplitudes de transition de n vers m: Anm = <m|A|n>

Attention

État propre |up> ne signifie PAS particule a spin vers le haut
Seulement que Si opérateur Spin(z) appliqué redonne même état, avec vp +1 (=1/2hbar)
Mais si opérateur Spin(x) appliqué, ne donne PAS zéro (composant x d’un vecteur sur z) mais ½ état x=+1 et ½ état x=-1
Donc danger à visualiser une petite flèche vers le haut!

Qubits

Espace vectoriel en 2 dimensions

Application K0 Ǩ0 vs. KL KS

Spin-isospin

Matrices de Pauli

Plusieurs qubits

Espace de Fock

La mesure

Projection d'un état

Observables

Commutateurs

Observables

À chaque propriété physique observable d'un système correspond un oéprateur hermitien sur l'espace vectoriel des états. C'est un postulat de la mécanique quantique, dont la conséquence est d'assurer que toutes les quantités mesurées qui sont des valeurs propres des opérateurs) sont des nombres réels et non complexes.

Valeur moyenne <Ψ|O|Ψ>

Vecteurs propres et valeurs propres O|λ_i> = λ_i |λ_i>

|Ψ> = Σ_i |λ_i><λ_i||Ψ> = Σ_i pi |λ_i> ⇒ <Ψ|O|Ψ> = Σ_i Σ_j pj* pi <λ_j|O| |λ_i> = Σ_i Σ_j p_j* p_i λ_i <λ_j|λ_i> = Σ_i p_i* p_i λ_i

Amplitude (de probabilité)

Amplitude de probabilité

Interférences

Ondes !

Probabilités = incertitude fondamentale?

= juste conséquence amplitude ≠ probabilité !

Physique classique = états non superposables -> inconnu ⇔ probabilités

Ici amplitude probab ≠ inconnu

Donc pas question d’incertitude (de qui d’aileurs?)

Ex « paquet d’ondes »

Double fente?

Les « dés » d’Einstein = conséquence du fait que les états appartiennent à un espace vectoriel

Ensemble complet d'observables qui commutent

Tout ce que l'on peut connaître simultanément d'un système quantique

Relations de Heisenberg

origine du quantum d'action h

du commutateur (égalité [X,P]=ih) à l'inégalité

incertitude, vraiment?

Opérateur hamiltonien

Particule libre

Etats libres et ondes planes

Puits carré

Quantum dans un puits carré

Effet tunnel

Oscillateur harmonique

Potentiel coulombien

Atome d'hydrogène

Schrödinger et Heisenberg

Représentations

Lexique Heisenberg ⇔ Schrödinger

Fonction d‘onde ψ(x) ⇔ <x|Ψ>

probabilités

Shut up and calculate!

« Limite classique »

Interprétation de de Broglie, Schrödinger et Bohm

Interprétation de Born

Interprétation "de Copenhague"

Influence sur Bohr de la philosophie de Kierkegaard (le philosophe ne peut être un observateur impartial détaché du monde sur lequel il construit sa philosophie, il est nécessairement un participant; la limite entre subjectivité et objectivité est purement arbitraire, et toute action est une suite de décisions modifiant le monde), ainsi que de la psychologie de William James (lequel souligne aussi l'absence de démarcation nette entre observateur et monde observé, ainsi que l'influence incontrôlable de l'observateur sur la situation qu'il observe). Influence également de Mach et des positivistes de l'École de Vienne: une assertion n'a de sens que si elle peut être vérifiée empiriquement (cf. Wittgenstein: "Ce dont on ne peut parler, il faut le taire").

Heisenberg résuma ce point de vue dans son livre Physique et philosophie en 1958.

La mécanique quantique comme théorie des probabilités

[D'après Scott Aaronson] Voir aussi le théorème de Gleason.

Selon Aaronson , la mécanique quantique n'est pas une théorie de la matière ou de l'énergie, des ondes ou des particules, mais une théorie qui traite de l'information, de ce qui est observable et des (amplitudes de) probabilités. Il soutient qu'elle aurait pu être inventée par les mathématiciens du 19° siècle s'ils avaient voulu géénraliser les probabilités des nombres réels positifs aux nombres complexes. Mais faute de pression expériementale, ce pas n'a pas été accompli. Aaronson présente aussi la mécanique quantique comme l'équivalent d'un système d'exploitation d'un ordinateur, la mécanique classique en étant un autre, les théories de l'électromagnétisme ou la thermodynamique étant alors l'équivalent de logiciels adaptés à ce système d'exploitation, et le portage d'une théorie d'un système à l'autre étant la "qauntification".

Les probabilités des événements 1, 2,… N étant p₁, p₂, …, p_N, on peut construire (au moins) deux théories des probabilités selon la norme utilisée:

1-norme |p_i| ➛ normalisation: ∑_i |p_i| =1
2-norme p_i² ➛ normalisation: ∑_i p_i² =1

Pour 2 événements (qu'on appellera pile et face avec une pièce de monnaie, |+> et |-> en mécanique quantique et 0 et 1 en informatique), les probabilités sont p et 1-p avec la 1-norme, et a et b (avec a²+b²=1) avec la 2-norme. La différence entre 1-norme et 2-norme devient apparente quand on effectue des transformations dans l'espace des états.

Pour un espace des états à 2 dimensions, les transformations possibles sont représentées par des matrices 2x2. Dans la théorie classique des probabilités, qui utilise la 1-norme, la matrice la plus générale transformant un vecteur de 1-norme 1 en vecteur de 1-norme 1 (pour conserver la probabilité) est une matrice (dite stochastique) dont les coefficients sont des nombres réels positifs et dont la somme des colonnes = 1. La permutation est ainsi représentée par la matrice P=(0 1, 1 0). Une matrice stochastique n'est pas nécessairement inversible, ce qui traduit une irréversibilité (une perte d'information).

Avec la 2-norme, la matrice la plus générale transformant un vecteur de 2-norme 1 en vecteur de 2-norme 1 (pour conserver la probabilité) est une matrice orthogonale (une matrice égale à la transposée de sa matrice inverse) si les coefficients sont des nombres réels, ou une matrice unitaire (égale à la transconjuguée de sa matrice inverse).

En employant la notation de Dirac, un qubit quelconque (une pièce de monnaie dont les probabilités suivent une 2-norme) peut s'écrire:

a|0>+b|1>

Une rotation de 45° (la "moitié" d'une rotation de 90° qui est une permutation des rôles) est représentée par la matrice

U = (1 -1 , 1 1)/√2

⇒ U |0> = {|0> + |1>}/√2 ⇒ état indéterminé?

⇒ U U |0> = {|0> + |1> – |0> + |1>}/2 = |1> ⇒ état déterminé?

La situation peut se décrire en termes de superposition d'états et d'interférences entre ceux-ci: appliquer U à l'état |0> conduit à une superposition des états |0> et |1>, l'appliquer une deuxième fois conduit à une interférence destructrice entre les états |0> et une interférence constructrice entre les états |1>.

Cette situation ne peut jamais se présenter avec des probabilités classiques (1-norme) qui sont toujours des nombres (réels) positifs et ne peuvent donc jamais se compenser.

Question: pourquoi ne pas utiliser une 3-norme, ou une 4-norme? Les seules transformations linéaires conservant une n-norme (∑_i [p_i|ⁿ =1) sont, à une phase près, les permutations des vecteurs de base pour n≠1 et n≠2, conduisant à des théories sans intérêt ("triviales"). Ceci rappelle le théorème de Fermat (xⁿ+yⁿ=zⁿ n'a de solution entière non triviale que pour n=1 et n=2). Généraliser à des transformations non-linéaires introduirait un comportement potentiellement chaotique où des vecteurs arbitrairement proches pourraient diverger de manière illimitée.

Question: pourquoi utiliser des nombres complexes? Pour que toute transformation linéaire unitaire U puisse être le produit de deux transformations linéaires unitaires V (i.e. V²=U), ce qui est l'équivalent d'une exigence de continuité des transformations, qu'elles puissent être éventuellement infinitésimales. La symétrie miroir U = (1 0, 0 -1) ne correspond à aucun V telle que V²=U, sauf à autoriser des coefficients complexes.

État à deux qubits

Ils sont engendrés par le produit tensoriels des espaces d'états à un qubit, et la base est donc formée des états |00>, |01>, |10> et |11>.

Certains états sont des produits d'états à 1 qubit:

(a|0> + b|1>) ⊗ (c|0> + d|1>) = ac|00> + ad|01> + bc|10> + bd|11>

Mais d'autres ne sont pas des produits d'états à 1 qubit, par exemple:

(|00> + |11>)/√2

un tel état est dit intriqué, ou non-séparable, et il est l'objet du paradoxe d'Einstein, Podolsky et Rosen.

Contact